
【题目】在平面直角坐标系中,已知直线AB 与y轴交于点A,与x轴交于点B,与双曲线y= ![]() (x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.
(x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.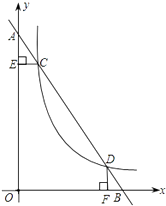
(1)求出m、n的值;
(2)求出直线AB的解析式;
(3)是否有△AEC≌△DFB,并说明理由.
【答案】
(1)
解:∵点C(1,6)和点D(3,n),
∴依题意得:m=6×1=6,
则n= ![]() =2,
=2,
故m=6,n=2

(2)
解:设直线AB的函数解析式为y=kx+b(k≠0)
由题意得 ![]() ,
,
解得: ![]() .
.
故直线AB的解析式为y=﹣2x+8
(3)
解:有△AEC≌△DFB,理由如下:
∵y=﹣2x+8
当x=0时,y=8;
当y=0时,﹣2x+8=0,
解得:x=4;
∴A(0,8),B (4,0),
∵CE⊥y轴于E,DF⊥x轴于F,
∴∠AEC=∠DFB=90°
∵A(0,8),B (4,0)C(1,6),D(3,2),
∴AE=8﹣6=2,DF=2,CE=1,BF=4﹣3=1,
∴AE=DF,CE=BF,
在△AEC和△DFB中,
 ,
,
∴△AEC≌△DFB(SAS).
【解析】(1)直接将C点坐标代入反比例函数解析式,进而得出m的值,进而求出n的值;(2)直接利用待定系数法求出直线AB的解析式;(3)利用已知解析式求出AE=DF,CE=BF,进而利用全等三角形的判定得出答案.


科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(时)之间的关系如图所示.以下说法错误的是( )
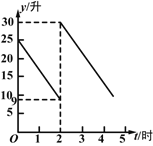
A. 加油前油箱中剩余油量y(升)与行驶时间t(时)之间的函数关系式是y=-8t+25
B. 途中加油21升
C. 汽车加油后还可行驶4小时
D. 汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司将5名员工分配至3个不同的部门,每个部门至少分配一名员工,其中甲、乙两名员工必须分配在同一个部门的不同分配方法数为( )
A.24
B.30
C.36
D.42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足 ![]() +(b2﹣16)2=0.
+(b2﹣16)2=0. 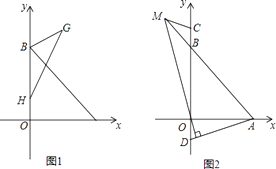
(1)求A、B两点的坐标,∠OAB的度数;
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,
①求点E到BH的距离;
②求点G的坐标;
(3)如图2,C,D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于多项式3x3y﹣4zy4+2x2y﹣1,下面说法正确的是( )
A.项分别是3x3y,4xy4 , 2x2y
B.多项式的次数是4次
C.按x的升幂排列是1﹣4xy4+2x2y+3x3y
D.这是个5次4项式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”. 数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由. ①摆出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com