
已知抛物线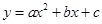 与
与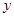 轴交于
轴交于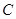 点,与
点,与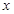 轴交于
轴交于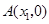 ,
,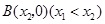 两点,顶点
两点,顶点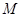 的纵坐标为
的纵坐标为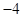 ,若
,若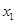 ,
, 是方程
是方程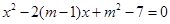 的两根,且
的两根,且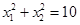 .
.
(1)求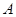 ,
,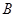 两点坐标;
两点坐标;
(2)求抛物线表达式及点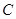 坐标;
坐标;
(3)在抛物线上是否存在着点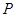 ,使△
,使△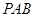 面积等于四边形
面积等于四边形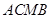 面积的2倍,若存在,求出
面积的2倍,若存在,求出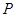 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
(1)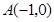 ,
,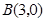 ;(2)
;(2)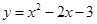 ,
, 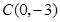 ;
;
(3)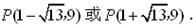
【解析】
试题分析:(1)根据韦达定理可得出A、B两点横坐标的和与积,联立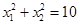 ,可求出m的值,进而可求出A、B的坐标.
,可求出m的值,进而可求出A、B的坐标.
(2)根据A、B的坐标,可得出抛物线的对称轴的解析式,即可求出其顶点M的坐标,根据得出的A、B、M三点的坐标,即可用待定系数法求出抛物线的解析式.
(3)可先求出四边形ACMB的面积(由于四边形ACMB不规则,因此其面积可用分割法进行求解).然后根据ACMB的面求出P点的纵坐标的绝对值,将其代入抛物线的解析式中即可求出P点的坐标.
(1)由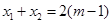 ,
,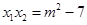 ,
,
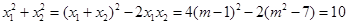 ,得
,得 ,
,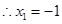 ,
,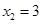 ,
,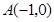 ,
,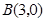 .
.
(2) 抛物线过
抛物线过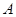 ,
,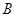 两点,其对称轴为
两点,其对称轴为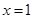 ,顶点纵坐标为
,顶点纵坐标为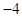 ,
,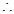 抛物线为
抛物线为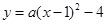 .
.
把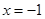 ,
,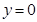 代入得
代入得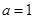 ,
, 抛物线函数式为
抛物线函数式为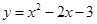 ,其中
,其中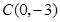 .
.
(3)存在着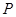 点.
点.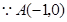 ,
,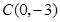 ,
,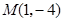 ,
,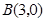 ,
,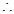
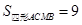 ,
,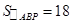 ,
,
即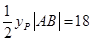 .
.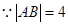 ,
,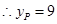 .把
.把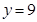 代入抛物线方程得
代入抛物线方程得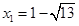 ,
,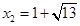 ,
,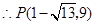 或
或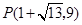 .
.
考点:本题考查的是二次函数的应用
点评:解答本题的关键是熟练掌握一元二次方程根与系数的关系,二次函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力.


科目:初中数学 来源: 题型:
在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,顶点为
,顶点为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求此时抛物线顶点
,求此时抛物线顶点![]() 的坐标;
的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线![]() 的解析式;
的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点![]() 恰好落在直线
恰好落在直线![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线与![]() 轴交于点
轴交于点![]() ,
,![]() ,与y轴交于点
,与y轴交于点![]() .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交![]() 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与 轴交于点
轴交于点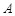 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与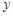 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为 .
.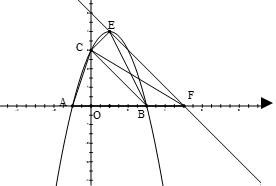
 的坐标;
的坐标; 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: . 轴交于点M、N,与
轴交于点M、N,与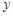 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式查看答案和解析>>
科目:初中数学 来源: 题型:
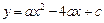 与
与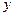 轴交于点
轴交于点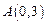 ,点
,点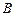 是抛物线上的点,且满足
是抛物线上的点,且满足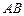 ∥
∥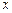 轴,点
轴,点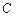 是抛物线的顶点.
是抛物线的顶点.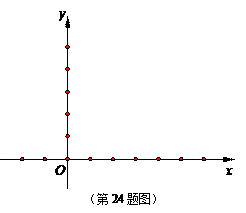
 点坐标;
点坐标;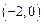 ,求抛物线的表达式;
,求抛物线的表达式;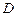 在线段
在线段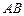 上,若以点
上,若以点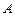 、
、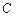 、
、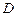 为顶点的三角形与
为顶点的三角形与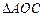 相似,试求点
相似,试求点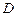 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
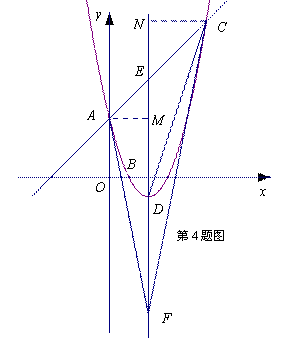
如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com