
【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
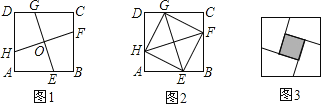
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为 cm2.
【答案】(1)四边形EFGH是正方形.证明见解析;(2)1.
【解析】
试题分析:(1)先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.
(2)根据已知条件,可以知道重新拼成的四边形是正方形(因为正方形GHEF的对角线翻到了外边,做了新拼成的正方形的边长),利用勾股定理求出GF和GO、FO的长,所的面积是10减去4个四边形GOFC的面积就是阴影部分的面积.
解:(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形.
(2)∵HA=EB=FC=GD=1,AB=BC=CD=AD=3,
∴GF=EF=EH=GH=![]() ,
,
∵由(1)知,四边形EFGH是正方形,
∴GO=OF,∠GOF=90°,
由勾股定理得:GO=OF=![]() ,
,
∵S四边形FCGO=![]() ×1×2+
×1×2+![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴S阴影=![]() ﹣S四边形FCGO×4=10﹣9=1.
﹣S四边形FCGO×4=10﹣9=1.



科目:初中数学 来源: 题型:
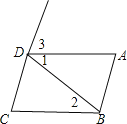
【题目】推理填空:如图:
①若∠1=∠2,
则 ∥ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 ∥ (同旁内角互补,两直线平行);
②当 ∥ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 ∥ 时,
∠3=∠C (两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
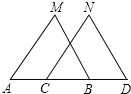
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
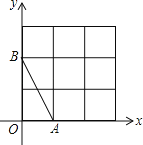
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有 个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2012m停下,则这个微型机器人停在( )

A.点A处 B.点B处 C.点C处 D.点E处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简(幂的运算)
(1).m3·m·(m2)3 (2).(p![]() q)4÷(q
q)4÷(q![]() p)3·(p
p)3·(p![]() q)2.
q)2.
(3).(![]() 3a3)3
3a3)3![]() a5·(
a5·(![]() 3a2)2 (4).22
3a2)2 (4).22![]() (
(![]() 2)-2
2)-2 ![]() 32÷(3.14
32÷(3.14![]()
![]() )0.
)0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com