
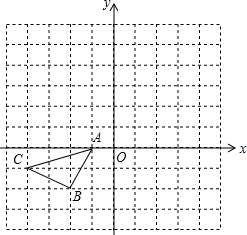
 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.分析 (1)利用关于原点对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出A、B、C的对应点A2、B2、C2,然后描点即可得到△A2B2C2,然后写出B2的坐标,再利用弧长公式计算出点C经过的路径长.
解答 解:(1)如图,△A1B1C1为所作,点B1坐标为(2,2);
(2)如图,△A2B2C2为所作,点B2的坐标为(2,-2),
AC=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
所以C经过的路径长=$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{17}}{2}$π.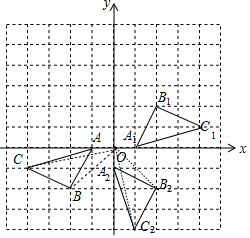
故答案为(2,2),(2,-2),$\frac{{\sqrt{17}}}{2}π$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
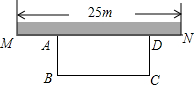 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com