设直线y=-0.5x+1与x轴、y轴分别交于点B、A,点C与点B关于y轴对称,以AC为直角边在第二象限作等腰Rt△ACD,过点D作DE⊥x轴于点E.若直线y=kx-2k将四边形OADE分为面积相等的两部分,则k= .
【答案】
分析:先确定A点坐标为(0,1),B点坐标为(2,0),点C的坐标为(-2,0),讨论:当AC为直角边,且∠DCA=90°时,根据等腰直角三角形的性质得CD=CA,∠DCA=90°,
,利用“AAS”可证明△ECD≌△OAC,则DE=OC=2,EC=OA=1,所以D点坐标(-3,2),然后确定OA的中点M的坐标,DE的中点N的坐标,MN的中点P的坐标,再P点坐标代入y=kx-2k得求出k的值;当AC为直角边,且∠CAD=90°时,如图2,作DF⊥y轴于F,同样的方法可确定D点坐标(-1,3),然后利用上述方法求对应k的值.
解答:解:把x=0代入y=-0.5x+1得y=1,把y=0代入y=-0.5x+1得-0.5x+1=0,解得x=2,则A点坐标为(0,1),B点坐标为(2,0)

∵点C与点B关于y轴对称,
∴点C的坐标为(-2,0),
当AC为直角边,且∠DCA=90°时,如图1,
M为OA的中点,N为DE的中点,P为MN的中点,则M(0,

)
∵△ACD为等腰直角三角形,
∴CD=CA,∠DCA=90°,
∴∠ECD+∠ACO=90°,
∵DE⊥x轴于点E,
∴∠ECD+∠EDC=90°,
∴∠EDC=∠ACO,
∵在△ECD和△OAC中
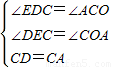
,
∴△ECD≌△OAC(AAS),
∴DE=OC=2,EC=OA=1,
∴OE=1+2=3,
∴D点坐标(-3,2),
∴N点坐标(-3,1),
∴P点坐标为(-

,

),
把P(-

,

)代入y=kx-2k得-

k-2k=

,解得k=-
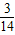
;
当AC为直角边,且∠CAD=90°时,如图2,作DF⊥y轴于F,同理可证得△FAD≌△OCA,
∴DF=OA=1,AF=OC=2,
∴OF=3,
∴D点坐标(-1,3),
∴N点坐标(-1,

),
∴P点坐标为(-

,

),
把P(-

,

)代入y=kx-2k得-

k-2k=

,解得k=-

;
∴k的值为-

或-

.
故答案为-

或-

.
点评:本题考查了一次函数的综合题:一次函数图象上点的坐标满足其解析式,会确定一次函数与坐标轴的交点坐标;同时运用三角形全等的知识解决线段相等的问题;理解直角梯形的重心的意义.


 )
)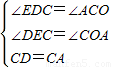 ,
, ,
, ),
), ,
, )代入y=kx-2k得-
)代入y=kx-2k得- k-2k=
k-2k= ,解得k=-
,解得k=-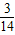 ;
; ),
), ,
, ),
), ,
, )代入y=kx-2k得-
)代入y=kx-2k得- k-2k=
k-2k= ,解得k=-
,解得k=- ;
; 或-
或- .
. 或-
或- .
.

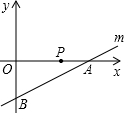 设一次函数y=0.5x-2的图象为直线m,m与x轴、y轴分别交于点A、B.
设一次函数y=0.5x-2的图象为直线m,m与x轴、y轴分别交于点A、B.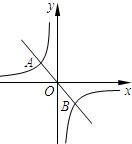 如图,设直线y=kx(k<0)与双曲线y=-
如图,设直线y=kx(k<0)与双曲线y=-