
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΓΔ
ΓΔ![]() Θ§ΫΜ
Θ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ°
Θ°
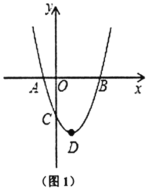
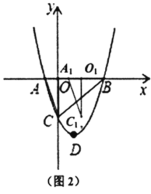
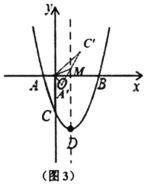
Θ®1Θ©≈ΉΈοœΏΕΞΒψ![]() ΒΡΉχ±ξΈΣ________ΘΜ
ΒΡΉχ±ξΈΣ________ΘΜ
Θ®2Θ©»γΆΦ2Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ°ΫΪ
Θ°ΫΪ![]() ―Ί
―Ί![]() ÷αΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ”“ΤΫ“ΤΒΟΒΫ
÷αΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ”“ΤΫ“ΤΒΟΒΫ![]() Θ§‘ΥΕ· ±ΦδΈΣ
Θ§‘ΥΕ· ±ΦδΈΣ![]() ΟκΘ°Β±
ΟκΘ°Β±![]() ±Θ§«σ
±Θ§«σ![]() ”κ
”κ![]() ÷ΊΒΰΟφΜΐ
÷ΊΒΰΟφΜΐ![]() ”κ
”κ![]() ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ«σ≥ω
ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ«σ≥ω![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»γΆΦ3÷–Θ§ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ“ΜΕ®ΒΡΫ«Ε»
Υ≥ ±’κ–ΐΉΣ“ΜΕ®ΒΡΫ«Ε»![]() ΒΟΒΫ
ΒΟΒΫ![]() Θ§±Ώ
Θ§±Ώ![]() ”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψ
”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψ![]() Θ°‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ“ΜΒψ
Θ°‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΥυ”–¬ζΉψΧθΦΰΒΡΒψ
ΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΥυ”–¬ζΉψΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() ΘΜΘ®2Θ©Β±
ΘΜΘ®2Θ©Β±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©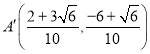 Μρ
Μρ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒψAΚΆΒψBΒΡΉχ±ξΩ…ΒΟΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣ![]() Θ§»ΜΚσΫΪΤδΜ·ΈΣΕΞΒψ ΫΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ§»ΜΚσΫΪΤδΜ·ΈΣΕΞΒψ ΫΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΗυΨίtΒΡ»Γ÷ΒΖΕΈßΖ÷άύΧ÷¬έΘ§»ΜΚσάϊ”Ο![]() ΒΡΟφΜΐΦθ»ΞΤδ”ύΗς»ΐΫ«–ΈΒΡΟφΜΐΦ¥Ω…Ζ÷±π«σ≥ω
ΒΡΟφΜΐΦθ»ΞΤδ”ύΗς»ΐΫ«–ΈΒΡΟφΜΐΦ¥Ω…Ζ÷±π«σ≥ω![]() ”κ
”κ![]() ΒΡΚ· ΐΫβΈω ΫΘ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ «σΉν÷ΒΦ¥Ω…ΘΜ
ΒΡΚ· ΐΫβΈω ΫΘ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ «σΉν÷ΒΦ¥Ω…ΘΜ
Θ®3Θ©»γΆΦΘ§…η![]() ΈΣ
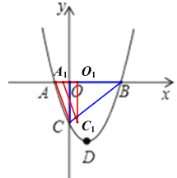
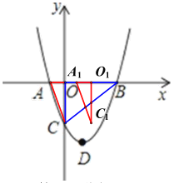
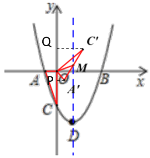
ΈΣ![]() Θ§ΒψMΈΣΘ®1Θ§mΘ©Θ§ΙΐΒψAΓδΉςAΓδPΓΆy÷α”ΎP,ΙΐΒψCΓδQΓΆy÷α”ΎQΘ§“Ή÷ΛΓςAΓδPOΓΉΓςOQCΓδΘ§Ν–≥ω±»άΐ ΫΦ¥Ω…«σ≥ωΒψCΓδΒΡΉχ±ξΘ§ΗυΨί»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ ΚΆΒ»Ϋ«Ε‘Β»±ΏΩ…÷Λ
Θ§ΒψMΈΣΘ®1Θ§mΘ©Θ§ΙΐΒψAΓδΉςAΓδPΓΆy÷α”ΎP,ΙΐΒψCΓδQΓΆy÷α”ΎQΘ§“Ή÷ΛΓςAΓδPOΓΉΓςOQCΓδΘ§Ν–≥ω±»άΐ ΫΦ¥Ω…«σ≥ωΒψCΓδΒΡΉχ±ξΘ§ΗυΨί»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ ΚΆΒ»Ϋ«Ε‘Β»±ΏΩ…÷Λ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§άϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωΒψMΒΡΉχ±ξΦ¥Ω…«σ≥ωΒψaΚΆbΘ§¥”Εχ«σ≥ωΒψAΓδΒΡΉχ±ξΘ°
ΒΡ÷–ΒψΘ§άϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωΒψMΒΡΉχ±ξΦ¥Ω…«σ≥ωΒψaΚΆbΘ§¥”Εχ«σ≥ωΒψAΓδΒΡΉχ±ξΘ°
Θ®1Θ©ΫβΘΚ”…“―÷Σ≈ΉΈοœΏ”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΓΔ
ΓΔ![]() Θ§
Θ§
ΓύΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣ![]()
Γύ![]() Θ§
Θ§
ΓύΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ°
Θ°
Θ®2Θ©ΫβΘΚΒ±x=0 ±Θ§y=-3
Υυ“‘ΒψCΒΡΉχ±ξΈΣΘ®0Θ§-3Θ©
ΔΌ»γΆΦΘ§Β±![]() ±Θ§
±Θ§
![]()
![]() Θ§
Θ§
ΓύΒ±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() ΘΜ
ΘΜ
ΔΎ»γΆΦΘ§Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓύΒ±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() ΘΜ
ΘΜ
ΓΏ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() Θ°
Θ°
Θ®3Θ©ΫβΘΚ»γΆΦΘ§…η![]() ΈΣ
ΈΣ![]() Θ§ΒψMΈΣΘ®1Θ§mΘ©Θ§ΙΐΒψAΓδΉςAΓδPΓΆy÷α”ΎP,ΙΐΒψCΓδQΓΆy÷α”ΎQΘ§“Ή÷ΛΓςAΓδPOΓΉΓςOQCΓδ
Θ§ΒψMΈΣΘ®1Θ§mΘ©Θ§ΙΐΒψAΓδΉςAΓδPΓΆy÷α”ΎP,ΙΐΒψCΓδQΓΆy÷α”ΎQΘ§“Ή÷ΛΓςAΓδPOΓΉΓςOQCΓδ
Γύ![]()
Ω…ΒΟ![]() Θ°
Θ°
–ΐΉΣΙΐ≥Χ÷–Θ§»τ¥φ‘Ύ“ΜΒψ![]() ΙΒΟ
ΙΒΟ![]() Θ§‘ρ
Θ§‘ρ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Γύ![]()
ΫβΒΟΘΚm=![]()
Γύ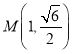 Μρ
Μρ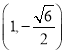
Γύ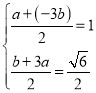 Μρ
Μρ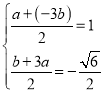
ΫβΒΟΘΚ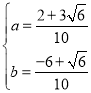 Μρ
Μρ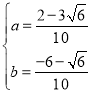
Γύ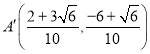 Μρ
Μρ Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
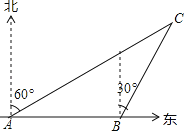
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΥ“”φ¥§“‘60ΚΘάοΟΩ–Γ ±ΒΡΥΌΕ»œρ’ΐΕΪΖΫœρΚΫ––Θ°‘ΎA¥Π≤βΒΟΒΤΥΰC‘Ύ±±ΤΪΕΪ60ΓψΖΫœρ…œΘΜΦΧ–χΚΫ––1–Γ ±ΒΫ¥οB¥ΠΘ§¥Υ ±≤βΒΟΒΤΥΰC‘Ύ±±ΤΪΕΪ30ΓψΖΫœρ…œΘ°“―÷Σ‘ΎΒΤΥΰC÷ήΈß50ΚΘάοΖΕΈßΡΎ”–ΑΒΫΗΘ§Έ ’βΥ“”φ¥§ΦΧ–χœρΕΪΚΫ––”–Έό¥ΞΫΗΒΡΈΘœ’ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
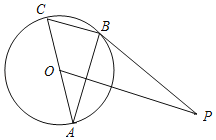
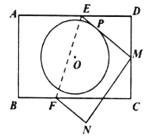
ΓΨΧβΡΩΓΩ»γΆΦΘ§AC «Γ―OΒΡ÷±ΨΕΘ§BC «Γ―OΒΡœ“Θ§ΒψP «Γ―OΆβ“ΜΒψΘ§Ν§Ϋ”PBΓΔABΘ§ΓœPBAΘΫΓœCΘ°
Θ®1Θ©«σ÷ΛΘΚPB «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©Ν§Ϋ”OPΘ§»τOPΓΈBCΘ§«“OPΘΫ4Θ§Γ―OΒΡΑκΨΕΈΣ![]() Θ§«σBCΒΡ≥ΛΘ°
Θ§«σBCΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΆΤΫχ»ΪΩΤ‘ΡΕΝΘ§≈ύ”ΐ ±¥ζ–¬»ΥΓ±Θ°Ρ≥―ß–ΘΈΣΝΥΗϋΚΟΒΊΩΣ’Ι―ß…ζΕΝ ιΜνΕ·Θ§ΥφΜζΒς≤ιΝΥΨ≈ΡξΦΕ50Οϊ―ß…ζΉνΫϋ“Μ÷ήΒΡΕΝ ι ±ΦδΘ§Ά≥ΦΤ ΐΨί»γœ¬±μΘΚ
±ΦδΘ®–Γ ±Θ© | 6 | 7 | 8 | 9 | 10 |
»Υ ΐ | 5 | 8 | 12 | 15 | 10 |
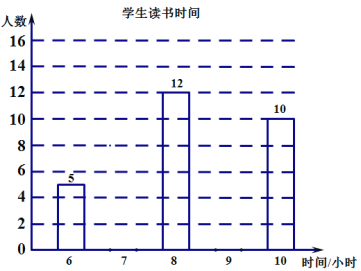
Θ®1Θ©ΗυΨί…œ ω±μΗώ≤Ι»Ϊœ¬ΟφΒΡΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©–¥≥ω’β50Οϊ―ß…ζΕΝ ι ±ΦδΒΡ÷Ύ ΐΓΔ÷–ΈΜ ΐΓΔΤΫΨυ ΐΘΜ
Θ®3Θ©»τΗΟ–Θ”–1000Οϊ―ß…ζΘ§«σΉνΫϋ“Μ÷ήΒΡΕΝ ι ±Φδ≤Μ…Ό”Ύ7–Γ ±ΒΡ»Υ ΐΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ°ΫΪΨΊ–Έ―Ί
Θ°ΫΪΨΊ–Έ―Ί![]() ’έΒΰΘ§ ΙΒψ
’έΒΰΘ§ ΙΒψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ±Ώ÷–Βψ
±Ώ÷–Βψ![]() ¥ΠΘ§Βψ
¥ΠΘ§Βψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ¥ΠΘ°Ν§Ϋ”
¥ΠΘ°Ν§Ϋ”![]() Θ§“‘ΨΊ–ΈΕ‘≥Τ÷––Ρ
Θ§“‘ΨΊ–ΈΕ‘≥Τ÷––Ρ![]() ΈΣ‘≤–ΡΒΡ‘≤”κ
ΈΣ‘≤–ΡΒΡ‘≤”κ![]() œύ«–”ΎΒψ
œύ«–”ΎΒψ![]() Θ§‘ρ‘≤ΒΡΑκΨΕΈΣ________Θ°
Θ§‘ρ‘≤ΒΡΑκΨΕΈΣ________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§
±Θ§![]() ΘΜ
ΘΜ
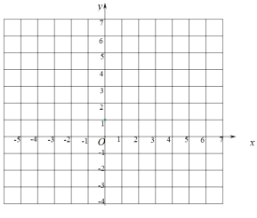
Θ®1Θ©ΗυΨίΗχΕ®ΒΡΧθΦΰΘ§‘ρ![]() _________Θ§
_________Θ§![]() ____________Θ°
____________Θ°
Θ®2Θ©‘ΎΗχ≥ωΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Μ≠≥ωΚ· ΐΆΦœώΘΜ
Θ®3Θ©ΔΌΫαΚœΥυΜ≠ΒΡΆΦœώΘ§÷±Ϋ”–¥≥ωΖΫ≥Χ![]() ΒΡΫβΘ§ΫβΈΣ________________Θ°Θ®ΨΪ»ΖΒΫ °Ζ÷ΈΜΘ©
ΒΡΫβΘ§ΫβΈΣ________________Θ°Θ®ΨΪ»ΖΒΫ °Ζ÷ΈΜΘ©
ΔΎ»τ“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœώ”κ
ΒΡΆΦœώ”κ![]() ΒΡΆΦœώ”–«“÷Μ”–»ΐΗωΫΜΒψΘ§‘ρ
ΒΡΆΦœώ”–«“÷Μ”–»ΐΗωΫΜΒψΘ§‘ρ![]() ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
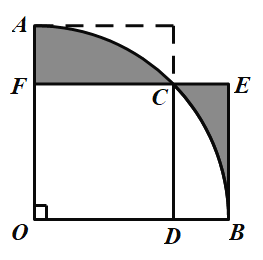
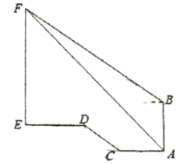
ΓΨΧβΡΩΓΩ»γΆΦΘ§…»–ΈAOBΒΡ‘≤–ΡΫ«ΈΣ÷±Ϋ«Θ§±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈODCFΒΡΕΞΒψFΘ§DΘ§CΖ÷±π‘ΎOAΘ§OBΘ§![]() …œΘ§ΙΐΒψBΉςBEΓΆFCΘ§ΫΜFCΒΡ―”≥ΛœΏ”ΎΒψEΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΒ»”Ύ__Θ°
…œΘ§ΙΐΒψBΉςBEΓΆFCΘ§ΫΜFCΒΡ―”≥ΛœΏ”ΎΒψEΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΒ»”Ύ__Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―ß–ΘΡ≥ ΐ―ß–Υ»Λ–ΓΉιœκ≤β―ß–ΘΤλΗΥΗΏΕ»»γΆΦΘ§ΟςΟς‘ΎΒΨœψ‘Α“Μ¬Ξ![]() Βψ≤βΒΟΤλΗΥΕΞΒψ
Βψ≤βΒΟΤλΗΥΕΞΒψ![]() ―ωΫ«ΈΣ
―ωΫ«ΈΣ![]() Θ§‘ΎΒΨœψ‘ΑΕΰ¬Ξ
Θ§‘ΎΒΨœψ‘ΑΕΰ¬Ξ![]() Βψ≤βΒΟΒψ
Βψ≤βΒΟΒψ![]() ΒΡ―ωΫ«ΈΣ
ΒΡ―ωΫ«ΈΣ![]() Θ°ΟςΟς¥”
Θ°ΟςΟς¥”![]() Βψ≥·ΤλΗΥΖΫœρ≤Ϋ––
Βψ≥·ΤλΗΥΖΫœρ≤Ϋ––![]() ΟΉΒΫ
ΟΉΒΫ![]() ΒψΘ§―ΊΤ¬Ε»
ΒψΘ§―ΊΤ¬Ε»![]() ΒΡΧ®ΫΉΉΏΒΫΒψ
ΒΡΧ®ΫΉΉΏΒΫΒψ![]() Θ§‘Όœρ«ΑΉΏ
Θ§‘Όœρ«ΑΉΏ![]() ΟΉΒΫΤλΗΥΒΉ≤Ω
ΟΉΒΫΤλΗΥΒΉ≤Ω![]() Θ§“―÷ΣΒΨœψ‘Α
Θ§“―÷ΣΒΨœψ‘Α![]() ΗΏΕ»ΈΣ
ΗΏΕ»ΈΣ![]() ΟΉΘ§‘ρΤλΗΥ
ΟΉΘ§‘ρΤλΗΥ![]() ΒΡΗΏΕ»‘ΦΈΣΘ® Θ©Θ®≤ΈΩΦ ΐΨίΘΚ
ΒΡΗΏΕ»‘ΦΈΣΘ® Θ©Θ®≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ©
Θ©
A.![]() ΟΉB.
ΟΉB.![]() ΟΉC.
ΟΉC.![]() ΟΉD.
ΟΉD.![]() ΟΉ
ΟΉ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
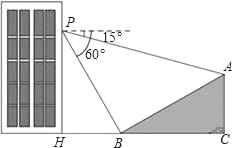
ΓΨΧβΡΩΓΩ»γΆΦΘ§–ΓΟς‘Ύ¥σ¬Ξ30ΟΉΗΏΘ®Φ¥PHΘΫ30ΟΉΘ©ΒΡ¥ΑΩΎP¥ΠΫχ––Ιέ≤βΘ§≤βΒΟ…ΫΤ¬…œA¥ΠΒΡΗ©Ϋ«ΓœAPQΈΣ15ΓψΘ§…ΫΫ≈B¥ΠΒΡΗ©Ϋ«ΓœBPQΈΣ60ΓψΘ§“―÷ΣΗΟ…ΫΤ¬ΒΡΤ¬Ε»iΘ®Φ¥tanΓœABCΘ©ΈΣ1ΘΚ![]() Θ§ΒψPΘ§HΘ§BΘ§CΘ§A‘ΎΆ§“ΜΗωΤΫΟφ…œΘ§ΒψHΓΔBΓΔC‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§«“PH¹AHCΘ°
Θ§ΒψPΘ§HΘ§BΘ§CΘ§A‘ΎΆ§“ΜΗωΤΫΟφ…œΘ§ΒψHΓΔBΓΔC‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§«“PH¹AHCΘ°
Θ®1Θ©«σ≥ω…ΫΤ¬Τ¬Ϋ«Θ®ΓœABCΘ©ΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σAΓΔBΝΫΒψΦδΒΡΨύάκΘ®ΫαΙϊΨΪ»ΖΒΫ0.1ΟΉΘ§≤ΈΩΦ ΐΨίΘΚ![]() Γ÷1.732Θ©Θ°
Γ÷1.732Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com