直线y=-2x+4分别交x轴、y轴于A、B两点,O是原点.
(1)求△ABO的面积;
(2)过三角形AOB的顶点能不能画出直线把△ABO分成面积相等的两部分?如能,可以画出几条?写出这样的直线所对应的函数关系式.
分析:(1)△ABO的面积S=
OA•OB,找出A、B两点坐标即可求出△ABO的面积;
(2)先设出该直线的解析式,分别从不同定点计算,看是否存在这种直线.
解答:解:(1)如图:直线y=-2x+4分别交x轴、y轴于A、B两点,
∴A(2,0),B(0,4).
即OB=|4-0|=4,OA=|-2-0|=2,
S
△ABO=
OA•OB=
×4×2=4;
(2)过三角形AOB的顶点能画出直线把△ABO分成面积相等的两部分,这样的直线可以画出3条.
①△ABO的OB边上的中线AC可把△ABO分成面积相等的两部分.
∵OB=4C是OB的中点,
∴C(0,2).
设直线AC的解析式为y=k
1x+b
1.
根据题意,得
,
解得
.
即直线AC的解析式为y=x+2;
②△ABO的OA边上的中线BD可把△ABO分成面积相等的两部分.
∵OA=2,D是OA的中点,
∴D(1,0).
设直线BD的解析式为y=k
2x+b
2.
根据题意,得
,
解得
.
即直线BD的解析式为y=-4x+4;
③△ABO的AB边上的中线OE可把△ABO分成面积相等的两部分.
根据三角形的中位线可求得E(1,2).
设直线BD的解析式为y=k
3x+b
3.
根据题意,得
,
解得
.
即直线OE的解析式为y=2x.
点评:本题主要考查对于一次函数图象的应用和二元一次方程组的掌握.



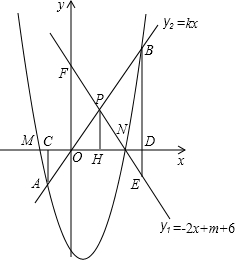 两侧,点N在点M的右边,直线y1=-2x+m+6经过点N,交y轴于点F.
两侧,点N在点M的右边,直线y1=-2x+m+6经过点N,交y轴于点F.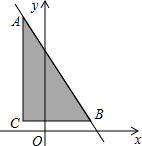 如图,在平面直角坐标系xOy中,点A、B都是直线y=-2x+m(m为常数)上的点,A、B的横坐标分别是-1,2,AC∥y轴,BC∥x轴,则三角形ABC的面积为( )
如图,在平面直角坐标系xOy中,点A、B都是直线y=-2x+m(m为常数)上的点,A、B的横坐标分别是-1,2,AC∥y轴,BC∥x轴,则三角形ABC的面积为( )