
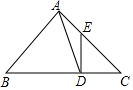
 在△ABC中,∠BAC=90°,∠B=45°,D为BC上一点,BD=AB,DE⊥BC,交AC于点E.
在△ABC中,∠BAC=90°,∠B=45°,D为BC上一点,BD=AB,DE⊥BC,交AC于点E.分析 (1)由BD=AB,得∠BAD=∠BDA,又因为∠BAC=90°,DE⊥BC,根据等角的余角相等,得∠EAD=∠ADE,从而问题得证;(2)由∠BAC=90°,DE⊥BC,∠B=45°,可得等腰三角形ABC、DEC,由 BD=AB,可得等腰三角形ABD.
解答 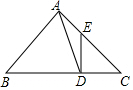 解:(1)证明:∵BD=AB,
解:(1)证明:∵BD=AB,
∴∠BAD=∠BDA
∵DE⊥BC,
∴∠BDE=90°
又∠BAC=90°,
∴∠EAD=∠EDA.
∴AE=DE,
即△ADE是等腰三角形.
(2)还有三个等腰三角形,△ABD、△ABC、△CDE.
点评 本题考查了等腰三角形的性质和判定及互余的性质.判断等腰三角形的办法:(1)根据定义,有两条边相等的三角形是等腰三角形;(2)根据性质,等角对等边.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
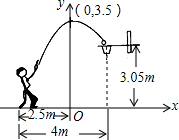 宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10,24,26 | B. | 15,20,25 | C. | 8,10,12 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
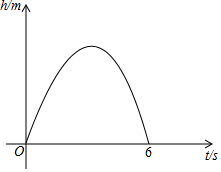 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
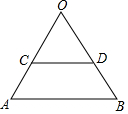 如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com