
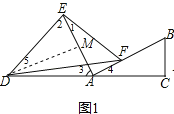
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
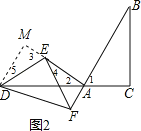
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
【答案】(1)![]() ;(2)见解析;(3)AE+AF=BC
;(2)见解析;(3)AE+AF=BC
【解析】
试题分析:(1)在等腰直角三角形DEF中,∠DEF=90°,求得∠1=20°,根据余角的定义得到∠2=∠DEF﹣∠1=70°,根据三角形的内角和得到∠3=60°,∠4=30°根据三角函数的定义得到cos∠4=![]() ,于是得到结论;
,于是得到结论;
(2)如图1,过D作DM⊥AE于D,在△DEM中,由余角的定义得到∠2+∠5=90°,由于∠2+∠1=90°,推出∠1=∠5证得△DEM≌△EFA,根据全等三角形的性质得到AF=EM,根据三角形的内角和和余角的定义得到∠3=∠B,推出△DAM≌△ABC,根据全等三角形的性质得到BC=AM即可得到结论;
(3)如图2,过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B,证得△ADM≌△BAC,由全等三角形的性质得到BC=AM,由于EF=DE,∠DEF=90°,推出∠4=∠5,证得△MED≌△AFE,根据全等三角形的性质得到ME=AF,即可得到结论.
解:(1)在等腰直角三角形DEF中,∠DEF=90°,
∵∠1=20°,
∴∠2=∠DEF﹣∠1=70°,
∵∠EDA+∠2+∠3=180°,
∴∠3=60°,
∵EA⊥AB,
∴∠EAB=90°,
∵∠3+∠EAB+∠A=180°,
∴∠4=30°,
∵∠C=90°,
∴cos∠4=![]() ,
,
∴AB=![]() =
=![]() =
=![]() ;
;
(2)如图1,过D作DM⊥AE于D,在△DEM中,∠2+∠5=90°,
∵∠2+∠1=90°,
∴∠1=∠5,
∵DE=FE,
在△DEM与△EFA中,
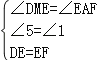 ,
,
∴△DEM≌△EFA,
∴AF=EM,
∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,
∴∠3+∠4=90°,
∴∠3=∠B,
在△DAM与△ABC中,
 ,
,
∴△DAM≌△ABC,
∴BC=AM,
∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,
∵∠C=90°,
∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,
∴∠2+∠1=90°,∠2=∠B,
在△ADM与△BAC中,
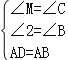 ,
,
∴△ADM≌△BAC,
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠3+∠DEF+∠4=180°,
∴∠3+∠4=90°,
∵∠3+∠5=90°,
∴∠4=∠5,
在△MED与△AFE中,
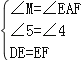 ,
,
∴△MED≌△AFE,
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.经过两点有且只有一条直线
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列三条线段中(单位长度都是cm),能组成三角形的是( )
A. 3,4,9 B. 50,60,12 C. 11,11,31 D. 20,30,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A(m,﹣2)、B(1,n﹣m)关于x轴对称,则m、n的值为( )
A. m=1,n=1 B. m=﹣1,n=1 C. m=1,n=3 D. m=1,n=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9 C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com