
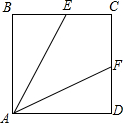
 如图,点E、F位于正方形ABCD边BC、CD上.
如图,点E、F位于正方形ABCD边BC、CD上.分析 (1)如图1中,延长AF、BC交于点M,作MH⊥AE交AE的延长线于H.设正方形的边长为3a,则BE=2a,EC=a,由△ABE∽△MHE,推出$\frac{AB}{BE}$=$\frac{MH}{HE}$=$\frac{3}{2}$,设HE=2k,MH=3k,
由tan∠MAH=$\frac{HM}{AH}$=$\frac{\sqrt{3}}{3}$,列出方程求出a,求出CM,再由CM∥AD,得到$\frac{CF}{DF}$=$\frac{CM}{AD}$,由此即可解决问题.
(2)如图2中,连接EF,作FM⊥AE于M.设正方形的边长为6a,则BE=EC=3a,DF=2a,CF=4a,AE=3$\sqrt{5}$a,AF=2$\sqrt{10}$a,由S△AEF=$\frac{1}{2}$•AE•FM=36a2-$\frac{1}{2}$•6a•3a-$\frac{1}{2}$•4a•3a-$\frac{1}{2}$•6a•2a=15a2,可得FM=2$\sqrt{5}$a,根据sin∠MAF=$\frac{MF}{AF}$,即可解决问题.
解答 解:(1)如图1中,延长AF、BC交于点M,作MH⊥AE交AE的延长线于H.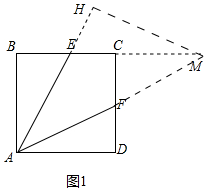
设正方形的边长为3a,则BE=2a,EC=a,
∵∠AEB=∠MEH,∠B=∠H=90°,
∴△ABE∽△MHE,
∴$\frac{AB}{BE}$=$\frac{MH}{HE}$=$\frac{3}{2}$,设HE=2k,MH=3k,
∵tan∠MAH=$\frac{HM}{AH}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{3k}{2k+\sqrt{13}a}$=$\frac{\sqrt{3}}{3}$,
∴k=$\frac{\sqrt{13}}{3\sqrt{3}-2}$a,
∴EM=$\sqrt{13}$k=$\frac{39\sqrt{3}+26}{23}$a,
∴CM=EM-EC=$\frac{39\sqrt{3}+3}{23}$a,
∵CM∥AD,
∴$\frac{CF}{DF}$=$\frac{CM}{AD}$=$\frac{\frac{39\sqrt{3}+3}{23}a}{3a}$=$\frac{13\sqrt{3}+1}{23}$.
(2)如图2中,连接EF,作FM⊥AE于M.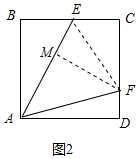
设正方形的边长为6a,则BE=EC=3a,DF=2a,CF=4a,AE=3$\sqrt{5}$a,AF=2$\sqrt{10}$a,
∵S△AEF=$\frac{1}{2}$•AE•FM=36a2-$\frac{1}{2}$•6a•3a-$\frac{1}{2}$•4a•3a-$\frac{1}{2}$•6a•2a=15a2,
∴FM=2$\sqrt{5}$a,
∴sin∠MAF=$\frac{MF}{AF}$=$\frac{2\sqrt{5}a}{2\sqrt{10}a}$=$\frac{\sqrt{2}}{2}$,
∴∠EAF=45°.
点评 本题考查正方形的性质、解直角三角形、锐角三角函数、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会利用参数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
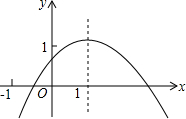 如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
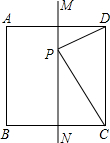 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
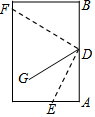 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
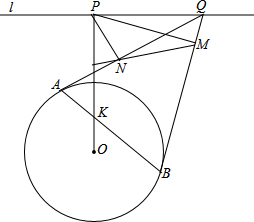 如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com