
已知抛物线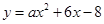 与直线
与直线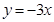 相交于点
相交于点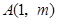 .
.
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到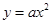 的图象?
的图象?
(3)设抛物线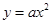 上依次有点
上依次有点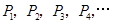 ,其中横坐标依次是
,其中横坐标依次是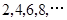 ,纵坐标依次为
,纵坐标依次为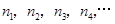 ,试求
,试求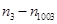 的值.
的值.
(1)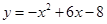 ;(2)把抛物线
;(2)把抛物线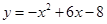 向左平移3个单位长度得到
向左平移3个单位长度得到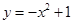 的图象,再把
的图象,再把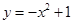 的图象向下平移1个单位长度得到
的图象向下平移1个单位长度得到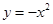 的图象;(3)4024000.
的图象;(3)4024000.
【解析】
试题分析:(1)先把 代入
代入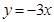 求得m的值,再代入
求得m的值,再代入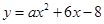 即可求得结果;
即可求得结果;
(2)先把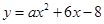 配方得到顶点式,再根据顶点坐标的变化分析即可;
配方得到顶点式,再根据顶点坐标的变化分析即可;
(3)根据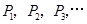 的横坐标是连续偶数,所以
的横坐标是连续偶数,所以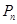 的横坐标是
的横坐标是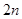 ,再代入函数解析式即得结果。
,再代入函数解析式即得结果。
(1)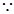 点
点 在直线
在直线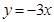 上,
上,
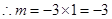 .
.
把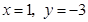 代入
代入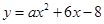 ,
,
得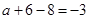 .求得
.求得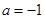 .
.
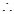 抛物线的解析式是
抛物线的解析式是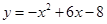 .
.
(2)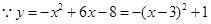 .
.
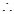 顶点坐标为
顶点坐标为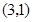 .
.
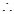 把抛物线
把抛物线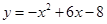 向左平移3个单位长度得到
向左平移3个单位长度得到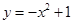 的图象,再把
的图象,再把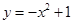 的图象向下平移1个单位长度得到
的图象向下平移1个单位长度得到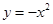 的图象.
的图象.
(3)由题意知,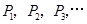 的横坐标是连续偶数,所以
的横坐标是连续偶数,所以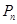 的横坐标是
的横坐标是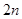 ,纵坐标为
,纵坐标为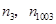 所对应的纵坐标依次是
所对应的纵坐标依次是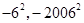 .
.
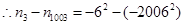
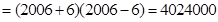 .
.
考点:本题考查的是二次函数的性质
点评:解答本题的关键是掌握函数图象上的点适合这个函数的解析式,同时掌握配方法求二次函数的顶点坐标的方法,另外也可熟记二次函数的顶点坐标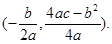


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
如图23,已知抛物线![]() 与
与![]() 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线![]() ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
1.填空:![]() =_______。
=_______。![]() =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
2.若线段BC的垂直平分线EF交BC于点E,交![]() 轴于点F.求FC的长;
轴于点F.求FC的长;
3.探究:在抛物线的对称轴上是否存在点P,使⊙P与![]() 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]()
![]() ,且
,且![]() 是方程
是方程![]() 的两个实数根,点
的两个实数根,点![]() 为抛物线与
为抛物线与![]() 轴的交点.
轴的交点.
(1)求![]() 的值;
的值;
(2)分别求出直线![]() 和
和![]() 的解析式;
的解析式;
(3)若动直线![]() 与线段
与线段![]() 分别相交于
分别相交于![]() 两点,则在
两点,则在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形(只求一种DE为腰或为底时)?若存在,求出点
为等腰直角三角形(只求一种DE为腰或为底时)?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 |
查看答案和解析>>
科目:初中数学 来源:2012届山东省宁津县实验中学九年级中考模拟数学试卷(带解析) 题型:解答题
如图23,已知抛物线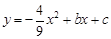 与
与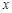 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线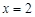 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
【小题1】填空: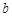 =_______。
=_______。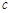 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
【小题2】若线段BC的垂直平分线EF交BC于点E,交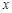 轴于点F.求FC的长;
轴于点F.求FC的长;
【小题3】探究:在抛物线的对称轴上是否存在点P,使⊙P与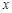 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考模拟数学试卷(解析版) 题型:解答题
如图23,已知抛物线 与
与 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
1.填空: =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
2.若线段BC的垂直平分线EF交BC于点E,交 轴于点F.求FC的长;
轴于点F.求FC的长;
3.探究:在抛物线的对称轴上是否存在点P,使⊙P与 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com