
【题目】如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
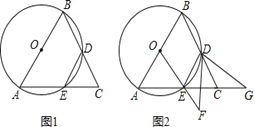
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
【答案】(1)证明见试题解析;(2)DF=DG.
【解析】
(1)利用院内接四边形的性质得到∠DEC=∠B,然后利用等角对等边得到结论.
(2)利用旋转的性质及圆内接四边形的性质证得△EDF≌△CDG后即可得到结论.
(1)∵四边形ABDE内接于⊙O,
∴∠B+∠AED=180°,
∵∠DEC+∠AED=180°,
∴∠DEC=∠B,
∵AB=AC,
∴∠C=∠B,
∴∠DEC=∠C,
∴DE=DC;
(2)∵四边形ABDE内接于⊙O,
∴∠A+∠BDE=180°,
∵∠EDC+∠BDE=180°,
∴∠A=∠EDC,
∵OA=OE,∴∠A=∠OEA,
∵∠OEA=∠CEF,∴∠A=∠CEF,∴∠EDC=∠CEF,
∵∠EDC+∠DEC+∠DCE=180°,∴∠CEF+∠DEC+∠DCE=180°,即∠DEF+∠DCE=180°,
又∵∠DCG+∠DCE=180°,∴∠DEF=∠DCG,
∵∠EDC旋转得到∠FDG,∴∠EDC=∠FDG,
∴∠EDC﹣∠FDC=∠FDG﹣∠FDC,即∠EDF=∠CDG,
∵DE=DC,∴△EDF≌△CDG(ASA),
∴DF=DG.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
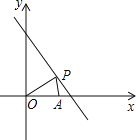
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
(1)根据下列所示图形写出一个代数恒等式 .
(2)已知正数a,b,c和m,n,l,满足ambnclk,试构造边长为k的正方形,利用图形面积来说明albmcnk2.
思考过程如下:
因为ambnclk,所以a,b,c,m,n,l,均 k(填“大于”或“小于”).由于k2可以看成一个正方形的面积,则al、bm、cn可以分别看成三个长方形的面积.请画出图形,并利用图形面积来说明albmcnk2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
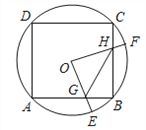
【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是![]() 上的一个动点(不与A、B重合),点F是
上的一个动点(不与A、B重合),点F是![]() 上的一点,连接OE、OF,分别与AB、BC交于点G、H,且∠EOF=90°,有下列结论: ①
上的一点,连接OE、OF,分别与AB、BC交于点G、H,且∠EOF=90°,有下列结论: ①![]() ; ②△OGH是等腰直角三角形; ③四边形OGBH的面积不随点E位置的变化而变化; ④△GBH周长的最小值为
; ②△OGH是等腰直角三角形; ③四边形OGBH的面积不随点E位置的变化而变化; ④△GBH周长的最小值为![]() .其中错误的是______.(把你认为错误结论的序号填上)
.其中错误的是______.(把你认为错误结论的序号填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,乙投放的这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)请用画树状图或列表的方法求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
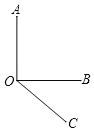
【题目】已知:射线OC在∠AOB的外部,如图,∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
(1)请在图中补全图形;
(2)求∠MON的度数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若千个完全相同的小正方体堆成的一个几何体![]() ,每个小正方体的边长为
,每个小正方体的边长为![]() ,如图所示.
,如图所示.
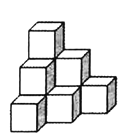
![]() 请画出这个几何体
请画出这个几何体![]() 的三视图. (用黑色水笔描清楚);
的三视图. (用黑色水笔描清楚);
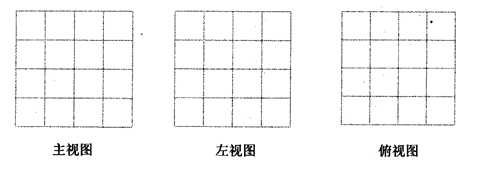
![]() 若将此几何体
若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则几何体
的表面喷上红漆(放在桌面上的一面不喷),则几何体![]() 上喷上红漆的面积为
上喷上红漆的面积为 ![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
![]() 若现在你的手头还有这样的一些边长为
若现在你的手头还有这样的一些边长为![]() 的小正方体可添放在几何体
的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com