
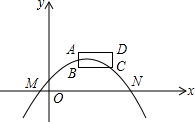
 如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④.
如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④. 分析 由抛物线的开口向下得到a<0,顶点坐标在第一象限得到b>0,抛物线与y轴的交点在y轴的上方推出c>0,由此即可判定abc的符号.由对称轴x=-$\frac{b}{2a}$>1,得到2a+b>0,由抛物线与直线y=k的交点情况得出方程ax2+bx+c-k=0总有两个不相等的实数根,顶点在矩形ABCD内部(包括边界),当顶点与A点重合,可以知道顶点坐标为(2,2);当顶点与C点重合,顶点坐标为(3,1),根据与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,列出不等式组,解不等式组可求a的取值,然后由此可判断a的取值范围.
解答 解:观察图形发现,抛物线的开口向下,
∴a<0,
∵顶点坐标在第一象限,
∴-$\frac{b}{2a}$>0,
∴b>0,
而抛物线与y轴的交点在y轴的上方,
∴c>0,
∴abc<0,故①正确;
∵点B的坐标为(2,1),BC=2,
∴C(4,1),
∵抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),
∴x=-$\frac{b}{2a}$>2,
∴-$\frac{b}{2a}$>1,
∵a<0,
∴-b<2a,
∴2a+b>0,故②错误;
由题意可知,抛物线与直线y=k(k<1)有两个交点,
∴当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;故③正确;
∵顶点在矩形ABCD内部(包括边界),
当顶点与A点重合,顶点坐标为(2,2),则抛物线解析式y=a(x-2)2+2,
由$\left\{\begin{array}{l}{a(-2-2)^{2}+2≤0}\\{a(-1-2)^{2}+2≥0}\end{array}\right.$,解得-$\frac{2}{9}$≤a≤-$\frac{1}{8}$;
当顶点与C点重合,顶点坐标为(4,1),则抛物线解析式y=a(x-4)2+1,
由$\left\{\begin{array}{l}{a(-2-4)^{2}+1≤0}\\{a(-1-4)^{2}+1≥0}\end{array}\right.$,解得-$\frac{1}{25}$≤a≤-$\frac{1}{36}$;
∵顶点可以在矩形内部,
∴-$\frac{2}{9}$≤a≤-$\frac{1}{36}$;故④正确;
故答案为①③④.
点评 本题主要考查了抛物线的解析式y=ax2+bx+c中a、b、c对抛物线的影响,在对于抛物线的顶点在所给图形内进行运动的判定,充分利用了利用形数结合的方法,展开讨论,加以解决.


科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:解答题
计算
(1)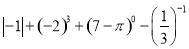 ;(2)(﹣a2)3﹣6a2•a4;
;(2)(﹣a2)3﹣6a2•a4;
(3)(x+1)2﹣(﹣x﹣2)(﹣x+2);(4)(2a﹣b﹣3)(2a+b﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
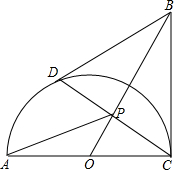 已知:如图,CA=CB,且CA⊥CB,以AC为直径作半圆⊙O,点D为半圆⊙O上的一点,BD=BC,连接OB,交线段CD于点P.
已知:如图,CA=CB,且CA⊥CB,以AC为直径作半圆⊙O,点D为半圆⊙O上的一点,BD=BC,连接OB,交线段CD于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
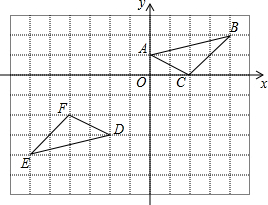 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )| A. | (-1,-1) | B. | (-1,-2) | C. | (-2,-1) | D. | (-2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
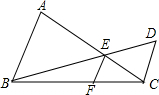 如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:
如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com