
【题目】已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).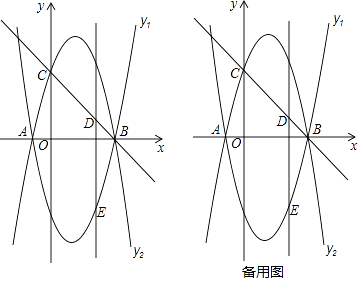
(1)求抛物线y1的函数解析式;
(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
【答案】
(1)解:将点A(﹣1,0)和点B(4,0)代入y1=ax2+bx﹣4得:a=1,b=﹣3,
∴抛物线y1的函数解析式为:y1=x2﹣3x﹣4;
(2)解:由对称性可知,抛物线y2的函数解析式为:y2=﹣x2+3x+4,
∴C(0,4),设直线BC的解析式为:y=kx+q,
把B(4,0),C(0,4)代入得,k=﹣1,q=4,
∴直线BC的解析式为:y=﹣x+4,
设D(m,﹣m+4),E(m,m2﹣3m﹣4),其中0≤m≤4,
∴DE=﹣m+4﹣(m2﹣3m﹣4)=﹣(m﹣1)2+9,
∵0≤m≤4,∴当m=1时,DEmax=9;
此时,D(1,3),E(1,﹣6);
(3)解:由题意可知,△BOC是等腰直角三角形,

∴线段BC的垂直平分线为:y=x,
由(2)知,直线DE的解析式为:x=1,
∴F(1,1),
∵H是BC的中点,
∴H(2,2),
∴DH= ![]() ,FH=
,FH= ![]() ,
,
∴S△DFH=1,
设⊙P的半径为r,
∵S⊙P:S△DFH=2π,
∴r= ![]() ,
,
∵⊙P与直线BC相切,
∴点P在与直线BC平行且距离为 ![]() 的直线上,
的直线上,
∴点P在直线y=﹣x+2或y=﹣x+6的直线上,
∵点P在抛物线y2=﹣x2+3x+4上,
∴﹣x+2=﹣x2+3x+4,
解得:x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
﹣x+6=﹣x2+3x+4,
解得:x3=2+ ![]() ,x4=2﹣
,x4=2﹣ ![]() ,
,
∴符合条件的点P坐标有4个,分别是(2+ ![]() ,﹣
,﹣ ![]() ),(2﹣
),(2﹣ ![]() ,
, ![]() ),(2+
),(2+ ![]() ,4﹣
,4﹣ ![]() ),(2﹣
),(2﹣ ![]() ,4+
,4+ ![]() ).
).
【解析】(1)(1)把A(﹣1,0)和点B(4,0)坐标代入抛物线解析式,利用待定系数法即可求出;(2)关于x轴翻折后的解析式可套用点关于x轴对称坐标变换方法即x不变,y变为其相反数-y ,-y=x2﹣3x﹣4,即y2=﹣x2+3x+4;竖直线段的最值问题可以化归为函数最值问题,须构建以动点D的横坐标m为自变量,DE长为因变量的函数,竖直线段等于上、下两端点的纵坐标之差来表示,二次函数最值问题可用配方法解决;(3)利用互垂直线的斜率积=-1求出BC的垂直平分线的解析式,由S⊙P:S△DFH=2π,得r= ![]() ,,由⊙P与直线BC相切,可知点P在与直线BC平行且距离为
,,由⊙P与直线BC相切,可知点P在与直线BC平行且距离为 ![]() 的直线上,由点P在直线y=﹣x+2或y=﹣x+6的直线上,点P在抛物线y2=﹣x2+3x+4上,联立解析式﹣x+2=﹣x2+3x+4和﹣x+6=﹣x2+3x+4,分别解方程即可.
的直线上,由点P在直线y=﹣x+2或y=﹣x+6的直线上,点P在抛物线y2=﹣x2+3x+4上,联立解析式﹣x+2=﹣x2+3x+4和﹣x+6=﹣x2+3x+4,分别解方程即可.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】抖音将“重庆洪崖洞”抖成了全国知名景点,五一期间,很多外地游客都慕名前来打卡.小丽和小萌二人约定分别从贵阳和遵义自驾到重庆游玩,由于贵阳到重庆的路程更远,所以小丽先出发,2.2小时后小萌才出发追赶小丽,她们二人离贵阳的距离![]() (千米)与小丽行驶的时间
(千米)与小丽行驶的时间![]() (小时)之间的关系图像如图所示,请根据图像回答下列问题:
(小时)之间的关系图像如图所示,请根据图像回答下列问题:
(1)小丽的速度为 千米/小时,小萌的速度为 千米/小时;
(2)当小萌追上小丽时,她们离贵阳的距离是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=_____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
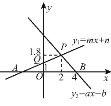
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:今有甲种袋子中装有黄金9枚(每枚黄金重量相同),乙种袋子中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲种袋子比乙种袋子轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可建立方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为10的半圆O,tan∠DBC= ![]() ,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.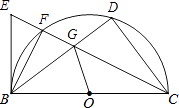
(1)求证:BE为⊙O切线;
(2)求证:BG2=FGCE;
(3)求OG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= ![]() 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )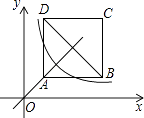
A.1<k<9
B.2≤k≤34
C.1≤k≤16
D.4≤k<16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com