
已知 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.

(1)求m和k的值
(2)若点C(-1,0),连结AC,BC,求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的 的取值范围.
的取值范围.
(1)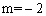 ,
,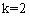 ;(2)3; (3)-1<x<0或x>2.
;(2)3; (3)-1<x<0或x>2.
【解析】
试题分析:(1)把A、B的坐标代入反比例函数解析式得出方程组,求出即可;
(2)求出A、B坐标,求出直线AB,求出直线AB和x轴交点坐标,根据三角形面积公式求出即可;
(3)根据A、B坐标结合图象求出即可.
试题解析:(1)∵A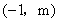 与B
与B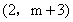 是反比例函数
是反比例函数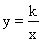 图象上的两个点,
图象上的两个点,
∴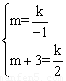 ,解得
,解得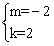 .
.
∴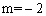 ,
,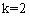 .
.
(2)由(1)得,A的坐标是(-1,-2),B的坐标是(2,1),
设直线AB的解析式是y=ax+b,则
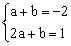 ,解得:
,解得: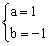 .
.
∴直线AB的解析式是y=x-1.
当y=0时,x=1,即OD=1.
∵C(-1,0),∴CD=2.
∴△ABC的面积是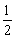 ×2×1+
×2×1+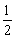 ×2×2=3.
×2×2=3.
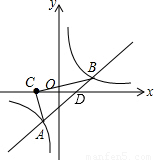
(3)一次函数的值大于反比例函数的值的x的取值范围是-1<x<0或x>2.
考点:反比例函数与一次函数的交点问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2007年初中毕业升学考试(江苏常州卷)数学(带解析) 题型:解答题
已知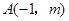 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.
(1)求 的值;
的值;
(2)若点 ,则在反比例函数
,则在反比例函数 图象上是否存在点
图象上是否存在点 ,使得以
,使得以 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年浙江省瑞安市初中毕业生学业考试适应性测试数学试卷(带解析) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)。
的坐标(能求出一个点即可)。
查看答案和解析>>
科目:初中数学 来源:2013届河南省郑州市第四中学九年级中招模拟数学试卷(带解析) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)
的坐标(能求出一个点即可)
|
查看答案和解析>>
科目:初中数学 来源:2012-2013学年河南省郑州市九年级中招模拟数学试卷(解析版) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。

(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)
的坐标(能求出一个点即可)
|
。
查看答案和解析>>
科目:初中数学 来源:2013年浙江省瑞安市毕业生学业考试适应性测试数学试卷(解析版) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。

(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)。
的坐标(能求出一个点即可)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com