
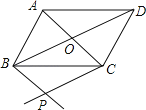
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.
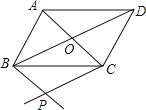
(1)判断四边形BPCO的形状,并说明理由;
(2)若将平行四边形ABCD改为菱形ABCD,其他条件不变,得到的四边形BPCO是什么四边形,并说明理由;
(3)若得到的是正方形BPCO,则四边形ABCD是 .(选填平行四边形、矩形、菱形、正方形中你认为正确的一个)
【答案】(1)四边形BPCO为平行四边形;(2)四边形BPCO为矩形;(3)四边形ABCD是正方形
【解析】
试题分析:(1)根据两组对边互相平行,即可得出四边形BPCO为平行四边形;
(2)根据菱形的对角线互相垂直,即可得出∠BOC=90°,结合(1)结论,即可得出四边形BPCO为矩形;
(3)根据正方形的性质可得出OB=OC,且OB⊥OC,再根据平行四边形的性质可得出OD=OB,OA=OC,进而得出AC=BD,再由AC⊥BD,即可得出四边形ABCD是正方形.
解:(1)四边形BPCO为平行四边形,理由如下:
∵BP∥AC,CP∥BD,
∴四边形BPCO为平行四边形.
(2)四边形BPCO为矩形,理由如下:
∵四边形ABCD为菱形,
∴AC⊥BD,则∠BOC=90°,
由(1)得四边形BPCO为平行四边形,
∴四边形BPCO为矩形.
(3)四边形ABCD是正方形,理由如下:
∵四边形BPCO是正方形,
∴OB=OC,且OB⊥OC.
又∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴AC=BD,
又∵AC⊥BD,
∴四边形ABCD是正方形.


科目:初中数学 来源: 题型:
【题目】甲乙两车间共120人,其中甲车间人数比乙车间人数的4倍少5人.
(1)求甲、乙两车间各有多少人?
(2)若从甲、乙两车间分别抽调工人,组成丙车间研制新产品,并使甲、乙、丙三个车间的人数比为13∶4∶7,那么甲、乙两车间要分别抽调多少工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(-1,1),(0,0)和(1,0).
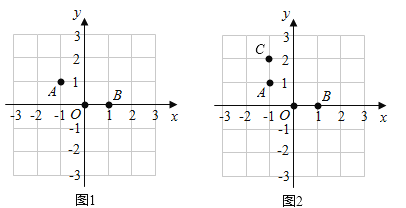
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表: 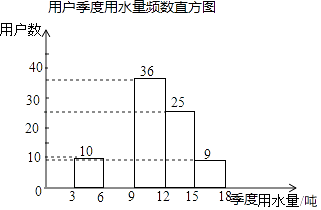
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= , n=;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
①若m=n,则|m|=|n|; ②若m=-n,则|m|=|-n|;
③若|-m|=|-n|,则m=-n; ④若|-m|=|-n|,则m=n.
A. ①② B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( ) 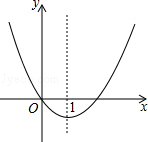
A.t≥﹣1
B.﹣1≤t<3
C.﹣1≤t<8
D.3<t<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(Ⅰ)直接写出点B坐标 ![]() ;判断△OBP的形状
;判断△OBP的形状 ![]() ;
;
(Ⅱ)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.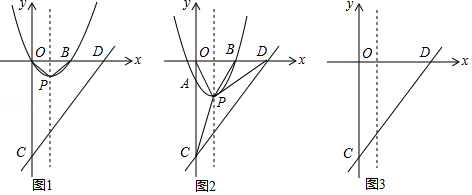
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com