在△ABC中.AC＝BC.∠C＝90°.将一块三角板的直角顶点放在斜边AB的中点P处.将三角板绕P点旋转.三角板的两条直角边分别交AC.CB于D.E两点.如图所示． (1)问PD与PE有何大小关系?并以图(2)为例加以说明, (2)在旋转过程中.还会存在与图不同的情形吗?若存在.请在图中PD与PE的大小关系在图(3)中是否还成立? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

在△ABC中，AC＝BC，∠C＝90°，将一块三角板的直角顶点放在斜边AB的中点P处，将三角板绕P点旋转，三角板的两条直角边分别交AC、CB于D、E两点，如图(1)、(2)所示．

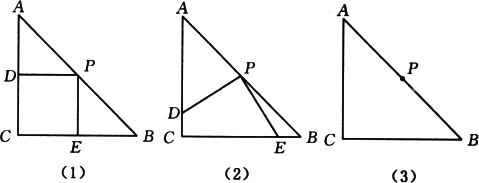
(1)问PD与PE有何大小关系？并以图(2)为例加以说明；

(2)在旋转过程中，还会存在与图(1)、(2)不同的情形吗？若存在，请在图(3)中画出，并说明(1)中PD与PE的大小关系在图(3)中是否还成立？

答案：
解析：

(1)PD＝PE．理由：连接CP．易说明△PCD≌△PBE，∴PD＝PE．(2)存在．如图所示，PD与PE仍然相等．理由：连接PC．∵∠CPD＝∠EPB，∠PCD＝∠PBE＝135°，PC＝PB，∴△PCD≌△PBE，∴PD＝PE．

练习册系列答案

好帮手阅读成长系列答案

超越训练系列答案

点石成金金牌每课通系列答案

68所名校图书毕业升学完全练考卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

操作：在△ABC中，AC＝BC＝2，∠C＝90⁰，将一块等腰三角形板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。研究：

（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。

（2）三角板绕点P旋转，是否能居为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。

（3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB＝1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图④加以证明。

查看答案和解析>>

科目：初中数学 来源：2012-2013学年江苏兴化市安丰中学八年级下学期第二次月考数学试卷（带解析） 题型：解答题

操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点（不包括射线的端点）.如图1，2，3是旋转三角板得到的图形中的3种情况.
研究：

（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合如图2加以证明；
（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长；若不能，请说明理由；
（3）若将三角板的直角顶点放在斜边AB上的M处，且AM∶MB＝1∶3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合如图4加以证明.

查看答案和解析>>

科目：初中数学 来源：2013届江苏省泰州市姜堰区四校八年级下学期第三次联考数学试卷（带解析） 题型：解答题

操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点（不包括射线的端点）.如图1，2，3是旋转三角板得到的图形中的3种情况.
研究：

⑴三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合如图2加以证明.
⑵三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长；若不能，请说明理由.
⑶若将三角板的直角顶点放在斜边AB上的M处，且AM∶MB＝1∶3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合如图4加以证明.