
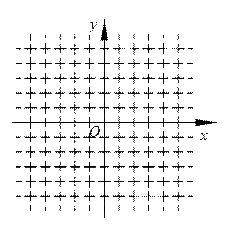
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
(本题10分)

(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(2)若点C是线段AB上任意一点,且AC=a,BC=b,点M、N分别是AC、BC的中点,请直接写出线段MN的长度;(结果用含a、b的代数式表示,并填入空格中)
(3)在(2)中,把点C是线段AB上任意一点改为:点C是射线AB上任意一点,其他条件不变,请在“备用图”上画出示意图,并求线段MN的长度,要求写出过程.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省张家港市九年级第一学期调研试卷数学卷 题型:解答题
(本题2分+3分+4分)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品每降低1元,其销量可增加10件。
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利y元。
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图象的变化趋势,结合题意写出该x取何值时,商场所获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省张家港市九年级第一学期调研试卷数学卷 题型:解答题
(本题2分+4分)已知函数 (
(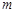 是常数).
是常数).
⑴求证:不论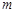 为何值,该函数的图象都经过
为何值,该函数的图象都经过 轴上的一个定点;
轴上的一个定点;
⑵若该函数的图象与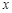 轴只有一个交点,求
轴只有一个交点,求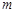 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(新疆乌鲁木齐卷)数学 题型:解答题
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒( ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山西卷)数学 题型:解答题
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒( ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com