
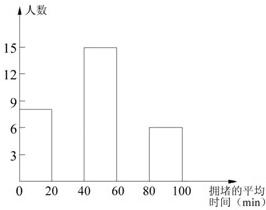
 图表.表中“0~20”表示拥堵的平均时间大于或等于0min而小于20min,其它类同.
图表.表中“0~20”表示拥堵的平均时间大于或等于0min而小于20min,其它类同.| 拥堵的平均时间/min | 频数/人数 | 频率 |
| 0~20 | 8 | 0.16 |
| 20~40 | a | 0.24 |
| 40~60 | 15 | 0.30 |
| 60~80 | 9 | b |
| 80~100 | 6 | 0.12 |
| 合计 | c | 1.00 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
 ,请说明理由.
,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 23、为响应“五个重庆”建设中的“畅通重庆”,沙坪坝区正积极发展公共交通.但就 目前仍存在的交通拥堵情况,重庆一中八年级一综合实践小组成员,在5月上旬的一天下午放学后,在汉渝路公交车站,随机调查了部分下车的乘客,统计了他们每 天上下班途中拥堵的平均时间,并绘制成如图表.表中“0~20”表示拥堵的平均 时间大于或等于0min而小于20min,其它类同.
23、为响应“五个重庆”建设中的“畅通重庆”,沙坪坝区正积极发展公共交通.但就 目前仍存在的交通拥堵情况,重庆一中八年级一综合实践小组成员,在5月上旬的一天下午放学后,在汉渝路公交车站,随机调查了部分下车的乘客,统计了他们每 天上下班途中拥堵的平均时间,并绘制成如图表.表中“0~20”表示拥堵的平均 时间大于或等于0min而小于20min,其它类同.| 拥堵的平均时间/min | 频数/人数 | 频率 |
| 0~20 | 8 | 0.16 |
| 20~40 | a | 0.24 |
| 40~60 | 15 | 0.30 |
| 60~80 | 9 | b |
| 80~100 | 6 | 0.12 |
| 合计 | c | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,请说明理由.
,请说明理由.查看答案和解析>>
科目:初中数学 来源:重庆市中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com