

分析 (1)作辅助线,构建全等三角形,证明△ABF≌△ACE,想办法得出DF=AD,从而得出结论;
(2)同理作辅助线,构建△ABF≌△ACE,则∠FAB=∠EAC,∠AEC=∠AFB,再证明∠AFB=∠AEC=∠BAE=∠FAD,根据等角对等边得DF=AD,由全等三角形对应边相等可知:CE=BF,所以CE=BD+AD;
(3)(1)的结论仍然成立,作辅助线构建△ABF≌△ACE,∠FAB=∠EAC,∠AEC=∠AFB,再证明AD=DF,则DF=BD+BF=BD+CE,所以AD=BD+CE.
解答 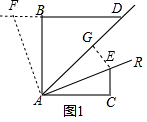 证明:(1)延长DB至F,使BF=CE,连接AF,
证明:(1)延长DB至F,使BF=CE,连接AF,
∵AB⊥BD,CE⊥AC,
∴∠ABF=∠ACE=90°,
∵AB=AC,
∴△ABF≌△ACE,
∴∠FAB=∠EAC,
由折叠得:△AGE≌△ACE,
∴∠GAE=∠EAC,
∴∠FAB=∠GAE=∠EAC,
∵∠BAC=90°,
∴∠BAG+∠GAE+∠EAC=90°,
∴∠BAG+∠FAB+∠GAE=90°,
∵∠F+∠FAB=90°,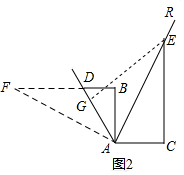
∴∠F=∠BAG+∠GAE,
∴∠F=∠BAG+∠FAB,
∴∠F=∠FAD,
∴DF=AD,
∴AD=BD+BF=BD+CE;
(2)(1)的结论不成立,存在CE=BD+AD,理由是:
如图2,延长BD至F,使BF=CE,连接AF,
∵∠ABF=∠ACE=90°,AB=AC,
∴△ABF≌△ACE,
∴∠FAB=∠EAC,∠AEC=∠AFB,
由折叠得:∠GAE=∠EAC,
∴∠FAB=∠GAE,
∴∠FAB-∠GAB=∠GAE-∠GAB,
即∠FAD=∠BAE,
∵∠BAC=90°,∠ACE=90°,
∴AB∥CE,
∴∠BAE=∠AEC,
∴∠AFB=∠AEC=∠BAE=∠FAD,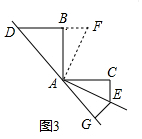
∴AD=DF,
∴CE=BF=BD+DF,
∴CE=BD+AD;
(3)如图3,当射线AR与射线AG都在∠BAC的外部时,(1)的结论仍然成立,
延长DB至F,使BF=CE,
∵AC=AB,∠ABF=∠ACE=90°,
∴△ABF≌△ACE,
∴∠F=∠AEC,∠BAF=∠EAC,
∴∠BAF+∠FAC=∠EAC+∠FAC=90°,
即∠FAE=90°,
∴∠GAE+∠DAF=90°,
由折叠得:∠GAE=∠EAC,
∴∠GAE=∠EAC=∠BAF,
∵∠ABF=90°,
∴∠F+∠BAF=90°,
∴∠F=∠DAF,
∴AD=DF,
∵DF=BD+BF=BD+CE,
∴AD=BD+CE.
点评 本题是几何变换的综合题,难度适中,考查了全等三角形的性质和判定、等腰三角形的性质和判定;在证明线段的和或差时,通常采用两类方法:①延长短边等于长边;②在长边上截取一线段等于短边,并构建三角形全等,从而得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
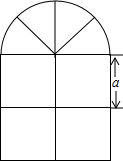 一个窗户的上部是一个半径为a的半圆形,一个窗户的上部分是4个扇形组成的半圆形,下部分是边长均为a的4个小正方形组成的.
一个窗户的上部是一个半径为a的半圆形,一个窗户的上部分是4个扇形组成的半圆形,下部分是边长均为a的4个小正方形组成的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
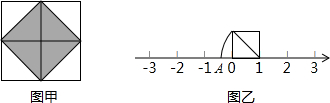
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
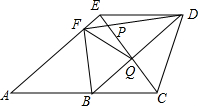 如图,四边形ACDE是梯形,四边形ABDE是平行四边形;点F在边AE上,DF、DB分别交CE于P、Q,如果△QCD的面积是30,△PDQ和△PEF的面积之差为16,那么四边形ABQF的面积是76.
如图,四边形ACDE是梯形,四边形ABDE是平行四边形;点F在边AE上,DF、DB分别交CE于P、Q,如果△QCD的面积是30,△PDQ和△PEF的面积之差为16,那么四边形ABQF的面积是76.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
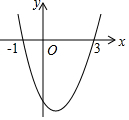 已知二次函数y=ax2+bx+c的图象如图,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b-2a=0,②abc<0,③2a-3b+4c<0,④8a+c>0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b-2a=0,②abc<0,③2a-3b+4c<0,④8a+c>0,其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com