
为了考查某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm)为16,9,14,,11,12,10,16,8,17,19,则这组数据的中位数和极差分别是( )
A. 13,11 B. 14,11 C. 12,11 D. 13,16
A 【解析】试题解析:将数据从小到大排列为:8,9,10,11,12,14,16,16,17,19, 中位数为:13; 极差=19?8=11. 故选A.科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
(1)计算:  ;
;
(2)解方程: 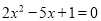 .
.
查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型:单选题
由3点30分到3点45分,时钟的分针转过的角度是( )
A. 30° B. 45° C. 60° D. 90°
D 【解析】时钟的分针每分钟转过的角度为6°, 所以,由3点30分到3点45分,时钟的分针转过的角度为:6°×(45-30)=90°, 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:填空题
已知⊙O半径为1,A、B在⊙O上,且 ,则AB所对的圆周角为__o.
,则AB所对的圆周角为__o.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:单选题
小明从二次函数 的图象(如图)中观察得到了下面五条信息:①
的图象(如图)中观察得到了下面五条信息:① ; ②
; ② ;③
;③ ;④
;④ ;则其中结论正确的个数是( )
;则其中结论正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
A 【解析】试题解析:①因为函数图象与y轴的交点在y轴的负半轴可知,c<0, 由函数图象开口向上可知,a>0,由①知,c<0, 由函数的对称轴在x的正半轴上可知, 故b<0,故abc>0;故此选项正确; ②因为函数的对称轴为故2a=?3b,即2a+3b=0;故此选项错误; ③因为图象和x轴有两个交点,所以,故此选项正确; ④把x=1代入得:a+b+c<0,故此选...查看答案和解析>>
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:解答题
为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?

查看答案和解析>>
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:解答题
计算:  .
.
查看答案和解析>>
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:单选题
剪纸是古老的汉族民间艺术,剪纸的工具材料简便普及,技法易于掌握,有着其他艺术门类不可替代的特性,因而,这一艺术形式从古到今,几乎遍及我国的城镇乡村,深得人民群众的喜爱.请你认真观察下列四幅剪纸图案,其中不是轴对称图形的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:单选题
若函数 的图象上有两点
的图象上有两点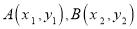 ,若
,若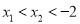 ,则( )
,则( )
A. 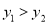 B.
B.  C.
C.  D.
D.  的大小不确定
的大小不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com