
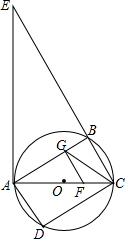
 如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.分析 (1)根据三个角是直角的四边形是矩形证明四边形ABCD是矩形,可得结论;
(2)证明△ABE∽△CBA,列比例式可得结论;
(3)根据F是AC的三等分点得:AG=2BG,设BG=x,则AG=2x,代入(2)的结论解出x的值,可得CD的长.
解答 证明:(1)∵AC为⊙O的直径,
∴∠ABC=∠ADC=90°,
∵∠BAD=90°,
∴四边形ABCD是矩形,
∴AB=CD;
(2)∵AE为⊙O的切线,
∴AE⊥AC,
∴∠EAB+∠BAC=90°,
∵∠BAC+∠ACB=90°,
∴∠EAB=∠ACB,
∵∠ABC=90°,
∴△ABE∽△CBA,
∴$\frac{AB}{BC}=\frac{BE}{AB}$,
∴AB2=BE•BC,
由(1)知:AB=CD,
∴CD2=BE•BC;
(3)∵F是AC的三等分点,
∴AF=2FC,
∵FG∥BE,
∴△AFG∽△ACB,
∴$\frac{AF}{FC}=\frac{AG}{BG}$=2,
设BG=x,则AG=2x,
∴AB=3x,
在Rt△BCG中,CG=$\sqrt{3}$,
∴BC2=($\sqrt{3}$)2-x2,
BC=$\sqrt{3-{x}^{2}}$,
由(2)得:AB2=BE•BC,
(3x)2=$\frac{9}{2}$$\sqrt{3-{x}^{2}}$,
4x4+x2-3=0,
(x2+1)(4x2-3)=0,
x=±$\frac{\sqrt{3}}{2}$,
∵x>0,
∴x=$\frac{\sqrt{3}}{2}$,
∴CD=AB=3x=$\frac{3\sqrt{3}}{2}$.
点评 本题是圆和四边形的综合题,难度适中,考查了矩形的性质和判定、平行相似的判定、三角形相似的性质、圆周角定理、切线的性质、勾股定理等知识,注意第2和3问都应用了上一问的结论,与方程相结合,熟练掌握一元高次方程的解法.


科目:初中数学 来源: 题型:解答题
 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) |
| 羽毛球 | 30 |
| 篮球 | a |
| 乒乓球 | 36 |
| 排球 | b |
| 足球 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象过点(1,0) | B. | y值随着x值增大而减小 | ||
| C. | 它的图象经过第二象限 | D. | 当x>1时,y>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
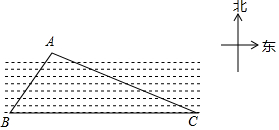 如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米.
如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
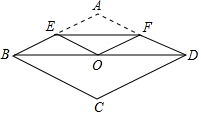 如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )| A. | 120° | B. | 100° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知平行四边形ABCD.
已知平行四边形ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com