
分析 利用勾股定理计算出BC=3.
(1)根据点与圆的位置关系,r=AC且r>OB;
(2)根据点与圆的位置关系,r<AC且r<OB;
(3)根据点与圆的位置关系,r<AC且r=OB,此时r不存在.
解答  解:∠C=90°,AC=4,AB=5,则BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
解:∠C=90°,AC=4,AB=5,则BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
(1)当r=4时,点A在⊙C上,且点B在⊙C内部;
(2)当3<r<4时,点A在⊙C外部,且点B在⊙C的内部;
(3)不存在实数r,使得点B在⊙C上,且点A在⊙C内部.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C是线段AB上的一点,D是线段CB的中点,已知AC=p,且p,q,r为质数,p<q,p+q=r,又知图中所有线段长度之和为27,则线段AB的长是( )
如图,C是线段AB上的一点,D是线段CB的中点,已知AC=p,且p,q,r为质数,p<q,p+q=r,又知图中所有线段长度之和为27,则线段AB的长是( )| A. | 8 | B. | 7 | C. | 6 | D. | 非上述答案 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
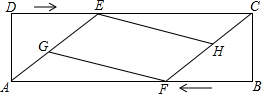 如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).
如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com