
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF. 
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
【答案】
(1)证明:在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中, 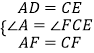 ,
,
∴△ADF≌△CEF(SAS)
(2)证明:由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形
【解析】(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.设该种冰箱每台的销售价降低了x元.
(1)填表:
每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
降价前 | 8 | |
降价后 |
(2)若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( ).
A.中国女排一定会夺冠B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大D.中国女排夺冠的可能性比较小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 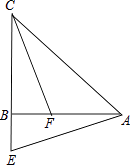
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请观察图形,并探究和解决下列问题:
(1)在第n个图形中,每一横行共有 个正方形,每一竖列共有 个正方形;
(2)在铺设第n个图形时,共有 个正方形;
(3)某工人需用黑白两种木板按图铺设地面,如果每块黑板成本为8元,每块白木板成本6元,铺设当n=5的图形时,共需花多少钱购买木板?

查看答案和解析>>
科目:初中数学 来源: 题型:
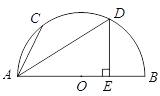
【题目】如图,C、D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4![]() ,DE⊥AB于E.
,DE⊥AB于E.
(1)求DE的长.
(2)求证:AC=2OE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com