
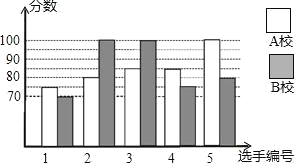
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
【答案】(1)85;85;80;(2)A校成绩好些;(3)A校代表队选手成绩较为稳定.
【解析】
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出A校、B校的方差即可.
解:(1)A校平均数为:![]() (75+80+85+85+100)=85(分),众数85(分);
(75+80+85+85+100)=85(分),众数85(分);
B校中位数80(分).
填表如下:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | 85 | 85 | 85 |
B校 | 85 | 80 | 100 |
故答案为:85;85;80.
(2)A校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些.
(3)∵A校的方差
s12=![]() [(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
B校的方差
s22=![]() [(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.
[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.
∴s12<s22,
因此,A校代表队选手成绩较为稳定.


科目:初中数学 来源: 题型:
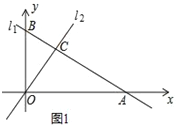
【题目】如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
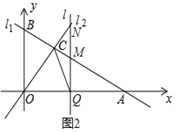
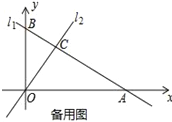
(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=3MN时,求t的值;
②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣ ![]() (x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.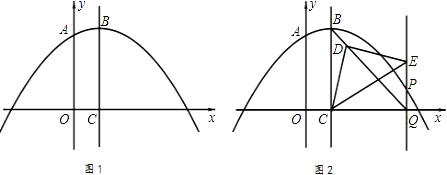
(1)如图1.求点A的坐标及线段OC的长;
(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上的一点且GH⊥EG.求证:PF∥GH.
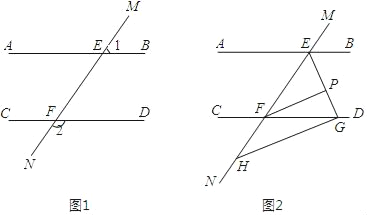
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).
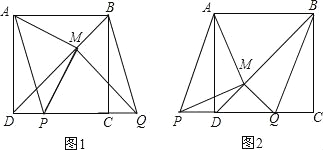
(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线![]() 绕原点
绕原点![]() 从数轴的正半轴逆时针旋转一定的角度
从数轴的正半轴逆时针旋转一定的角度![]() (
(![]() ),射线上的一点
),射线上的一点![]() 与原点
与原点![]() 的距离(
的距离(![]() )为
)为![]() ,并规定:当
,并规定:当![]() 或
或![]() 时,点
时,点![]() 的位置记作
的位置记作![]() ;当
;当![]() 时,点
时,点![]() 的位置记作
的位置记作![]() .如图,点
.如图,点![]() 、
、![]() 的位置表示为
的位置表示为![]() ,
,![]() .回答下列问题:
.回答下列问题:
(1)已知点![]() ,点
,点![]() ,则点
,则点![]() 与点
与点![]() 的距离为 ;线段
的距离为 ;线段![]() 的中点
的中点![]() 的位置是( , ).
的位置是( , ).
(2)已知点![]() ,点
,点![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,以每秒2个单位长度的速度在线段
点出发,以每秒2个单位长度的速度在线段![]() 上来回运动;同时射线
上来回运动;同时射线![]() 以每秒10°的速度绕原点
以每秒10°的速度绕原点![]() 逆时针旋转,当时间
逆时针旋转,当时间![]() (其中
(其中![]() )为何值时,
)为何值时,![]() ?并求出此时三角形
?并求出此时三角形![]() 的面积.
的面积.
(3)直接写出位置满足![]() 的所有点所围成的图形面积.(结果保留一位小数)
的所有点所围成的图形面积.(结果保留一位小数)
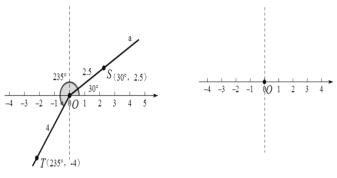
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=2 ![]() ,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为( )
,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为( ) 
A.4π
B.4 ![]() π
π
C.8π
D.8 ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE. 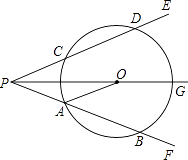
(1)求证:AP=AO;
(2)若tan∠OPB= ![]() ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 , 能构成等腰梯形的四个点为或或 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com