

���� ��1��������AC��BD�����ڵ�M�����P��Բ�������ǣ�x��y�����г�Բ�ĵ�M�Ĺ�ϵʽ����P1��0��-3����P2��4��6����P3��4$\sqrt{2}$��2�����룬���Ƿ�������涨���ڰ�y=-x+2����x2+��y-2��2=32�����x��y��ֵ����д�����꣮
��2�����������LIEΪ����ֱ�������Σ��õ�L��0��5���������ó���LOMΪ����ֱ�������Σ���P��p��-p+5���ݹ�ϵ�г���������Բ�ģ������꣬���ó��ҳ���������DH����DT��HF����DΪԲ�ģ�DEΪ�뾶��Բ����DT�ڵ�E1����HD��E2����0��r��DT-DE1ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ���r��HE2ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ��ݴ���⣮
��� �⣺��1��������AC��BD�����ڵ�M��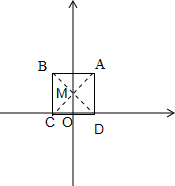
���ı���ABCD�������Σ�
��M��������ABCD�����߾��붼���
���Pһ��ͨ����M��
��A��2��4��
��M��0��2��
���P��Բ�������ǣ�x��y����
��r=4$\sqrt{2}$ʱ��
��x2+��y-2��2=��4$\sqrt{2}$��2��
����x2+��y-2��2=32��
��P1��0��-3����P2��4��6����P3��4$\sqrt{2}$��2�����룬ֻ��P2��P3������
����Գ�Ϊ������ABCD�ġ��Ⱦ�Բ����Բ�ĵ���P2��P3��
�ʴ�Ϊ��P2��P3��
�ڡߵ�P��ֱ��y=-x+2�ϣ��ҡ�P��������ABCD�ġ��Ⱦ�Բ����
���y=-x+2����x2+��y-2��2=32����x2+x2=32��
���x=��4��
��y=-2��6��
��P��4��-2����P��-4��6����
�ʴ�Ϊ����4��-2����P��-4��6����
��2������ͼ��
�١ߡ�PͬʱΪ������ABCD��������EFGH�ġ��Ⱦ�Բ����
���Pͬʱ��������ABCD�ĶԳ�����E��������EFGH�ĶԳ�����I��
���P���߶�EI���д����ϣ�
��A��2��4����������ABCD�ı�CD��x���ϣ�F��6��2����������EFGH�ı�HE��y���ϣ�
��E��0��2����I��3��5��
���IEH=45�㣬
���߶�EI���д�����y�ύ�ڵ�L����x�ύ�ڵ�M��
���LIEΪ����ֱ�������Σ�LI��y�ᣬ
��L��0��5����
���LOMΪ����ֱ�������Σ�LO=OM
��M��5��0����
��P��ֱ��y=-x+5�ϣ�
����P��p��-p+5��
��P��PQ��ֱ��BC��Q������PE��
�ߡ�P��BC����ֱ�����У�
��PE=PQ��
��p2+��-p+5-2��2=��p+2��2��
��ã�P1=5+2$\sqrt{5}$��P2=5-2$\sqrt{5}$��
��P1��5+2$\sqrt{5}$��-2$\sqrt{5}$����P2��5-2$\sqrt{5}$��2$\sqrt{5}$����
�ߡ�P����E����E����y���ϣ�
���P��y���Ͻصõ��ҳ�Ϊ2|-2$\sqrt{5}$-2|=4$\sqrt{5}$��2|2$\sqrt{5}$-2|=4$\sqrt{5}$-4��
����ͼ2������DH����DT��HF����DΪԲ�ģ�DEΪ�뾶��Բ����DT�ڵ�E1����HD��E2��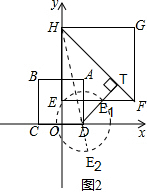
��0��r��DT-DE1ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��HF���ڵ�ֱ��Ϊ��y=-x+8��
DT���ڵ�ֱ��Ϊ��y=x-2��
��T��5��3����
��D��2��0����
��DT=$\sqrt{{3}^{2}+��5-2��^{2}}$=3$\sqrt{2}$��
��DE=DE1
��DT-DE1=DT-DE=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$��
�൱0��r��$\sqrt{2}$ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��r��HE2ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��HE2=HD+DE2��DE2=DE��
��HE2=HD+DE=$\sqrt{H{O}^{2}+O{D}^{2}}$+2$\sqrt{2}$=2$\sqrt{17}$+2$\sqrt{2}$��
�൱r��2$\sqrt{17}$+2$\sqrt{2}$ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
���Ͽ�֪��0��r��$\sqrt{2}$��r��2$\sqrt{17}$+2$\sqrt{2}$ʱ�߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
�ʴ�Ϊ��0��r��$\sqrt{2}$��r��2$\sqrt{17}$+2$\sqrt{2}$��
���� ���⿼��Բ���ۺ��⣬����Ĺؼ�����ȷ���⣬������Ŀ�������������������ʵĸ����ߣ��ҳ�����������Ҫ���������������ν�ϵ�˼�������⣮����Ա����еġ��Ⱦ�Բ���Ķ�����ȷ����Ҳ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC����D��BC�ϣ���AD=BD����ADB=100�㣬���DAC�Ķ���Ϊ60�㣮
��ͼ���ڡ�ABC�У�AB=AC����D��BC�ϣ���AD=BD����ADB=100�㣬���DAC�Ķ���Ϊ60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
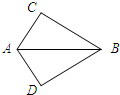 ��ͼ��AC=AD����������һ�����������ݡ��߽DZߡ��ж���ADB�ա�ACB���������ӵ������ǡ�CAB=��DAB��
��ͼ��AC=AD����������һ�����������ݡ��߽DZߡ��ж���ADB�ա�ACB���������ӵ������ǡ�CAB=��DAB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com