
°æƒø°ø2008ƒÍ5‘¬12»’£¨Àƒ¥® °∑¢…˙8.0º∂µÿ’£¨ƒ≥ –≈…≥ˆ¡Ω∏ˆ«¿œ’滑÷π§≥Ã∂”∏œµΩ„Î¥®÷ß‘Æ£¨º◊π§≥Ã∂”≥–µ£¡À2400√◊µ¿¬∑«¿–fi»ŒŒÒ£¨““π§≥Ã∂”±»º◊π§≥Ã∂”∂‡≥–µ£¡À600√◊µƒµ¿¬∑«¿–fi»ŒŒÒ£¨º◊π§≥Ã∂” ©π§ÀŸ∂»±»““π§≥Ã∂”√ø–° ±…Ÿ–fi40√◊£¨Ω·π˚¡Ωπ§≥Ã∂”Õ¨ ±ÕÍ≥…»ŒŒÒ£Æ
Œ º◊°¢““¡Ωπ§≥Ã∂”√ø–° ±∏˜«¿–fiµ¿¬∑∂‡…Ÿ√◊£Æ
£®1£©…Ë““π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑x√◊£¨‘Ú”√∫¨xµƒ Ω◊”±Ì æ£∫º◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑°° °°√◊£¨º◊π§≥Ã∂”ÕÍ≥…≥–µ£µƒ«¿–fi»ŒŒÒÀ˘–Ë ±º‰Œ™°° °°–° ±£¨““π§≥Ã∂”ÕÍ≥…≥–µ£µƒ«¿–fi»ŒŒÒÀ˘–Ë ±º‰Œ™°° °°–° ±£Æ
£®2£©¡–≥ˆ∑Ω≥ã¨ÕÍ≥…±æÃ‚Ω‚¥£Æ
°æ¥∞∏°ø£®1£©£®x©Å40£©£ª![]() £ª
£ª![]() £ª£®2£©º◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑160√◊£¨““π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑200√◊
£ª£®2£©º◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑160√◊£¨““π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑200√◊
°æΩ‚Œˆ°ø
£®1£©º◊∂”√ø–° ±±»““…Ÿ40√◊£¨µ√µΩº◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑£®x©Å40£©√◊£¨”√π§◊˜◊‹¡ø≥˝“‘π§◊˜–߬ µ√µΩº◊µƒ ±º‰Œ™![]() £¨““µƒ ±º‰Œ™
£¨““µƒ ±º‰Œ™![]() £ª
£ª
£®2£©∏˘æ›£®1£©º¥ø…¡–µ√∑Ω≥ã¨Ω‚∑Ω≥õ√µΩ¥∞∏.
£®1£©…Ë““π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑x√◊£¨‘Úº◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑£®x©Å40£©√◊£¨º◊π§≥Ã∂”ÕÍ≥…≥–µ£µƒ«¿–fi»ŒŒÒÀ˘–Ë ±º‰Œ™![]() –° ±£¨““π§≥Ã∂”ÕÍ≥…≥–µ£µƒ«¿–fi»ŒŒÒÀ˘–Ë ±º‰Œ™
–° ±£¨““π§≥Ã∂”ÕÍ≥…≥–µ£µƒ«¿–fi»ŒŒÒÀ˘–Ë ±º‰Œ™![]() £Ω
£Ω![]() –° ±£Æ
–° ±£Æ
π ¥∞∏Œ™£∫£®x©Å40£©£ª![]() £ª
£ª![]() £Æ
£Æ
£®2£©“¿Ã‚“‚£¨µ√£∫![]() £Ω
£Ω![]() £¨
£¨
Ω‚µ√£∫x£Ω200£¨
æ≠ºÏ—È£¨x£Ω200 «‘≠∑Ω≥õƒΩ‚£¨«“∑˚∫œÃ‚“‚£¨
°‡x©Å40£Ω160£Æ
¥£∫º◊π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑160√◊£¨““π§≥Ã∂”√ø–° ±«¿–fiµ¿¬∑200√◊£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄Rt°˜ABC÷–£¨°œACB=90°„£¨AC=15£¨AB=25£¨µ„DŒ™–±±flAB…œ∂ص„£Æ

£®1£©»ÁÕº1£¨µ±CD°ÕAB ±£¨«ÛCDµƒ≥§∂»£ª
£®2£©»ÁÕº2£¨µ±AD=AC ±£¨π˝µ„D◊˜DE°ÕABΩªBC”⁄µ„E£¨«ÛCEµƒ≥§∂»£ª
£®3£©»ÁÕº3£¨‘⁄µ„Dµƒ‘À∂Øπ˝≥Ã÷–£¨¡¨Ω”CD£¨µ±°˜ACDŒ™µ»—¸»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆADµƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—ß–£Œ™¡Àµ˜≤È—ß…˙∂‘Ω×ߵƒ¬˙“‚∂»£¨Àʪ˙≥È»°¡À≤ø∑÷—ß…˙◊˜Œ æ̵˜≤È£∫”√°∞A°±±Ì æ°∞∫‹¬˙“‚°∞£¨°∞B°±±Ì æ°∞¬˙“‚°±£¨°∞C°±±Ì æ°∞±»Ωœ¬˙“‚°±£¨°∞D°±±Ì æ°∞≤ª¬˙“‚°±£¨»ÁÕºº◊°¢““ «π§◊˜»À‘±∏˘æ›Œ æ̵˜≤ÈÕ≥º∆◊ ¡œªÊ÷∆µƒ¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«Îƒ„∏˘æ›Õ≥º∆ÕºÃ·π©µƒ–≈œ¢Ω‚¥“‘œ¬Œ £∫
£®1£©±æ¥ŒŒ æ̵˜≤È£¨π≤µ˜≤È¡À∂‡…Ÿ√˚—ß…˙£ø
£®2£©Ω´Õºº◊÷–°∞B°±≤ø∑÷µƒÕº–Œ≤π≥‰ÕÍ’˚£ª
£®3£©»Áπ˚∏√–£”–—ß…˙1000»À£¨«Îƒ„π¿º∆∏√–£—ß…˙∂‘Ω×ß∏–µΩ°∞≤ª¬˙“‚°±µƒ‘º”–∂‡…Ÿ»À£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄√¿ªØ–£‘∞µƒªÓ∂Ø÷–£¨ƒ≥–À»§–°◊ÈœÎΩË÷˙»ÁÕºÀ˘ 浃÷±Ω««ΩΩ«£®¡Ω±fl◊„πª≥§£©£¨”√28m≥§µƒ¿È∞ Œß≥…“ª∏ˆæÿ–Œª®‘∞ABCD£®¿È∞ ÷ªŒßAB£¨BC¡Ω±fl£©£¨…ËAB=m£Æ»Ù‘⁄P¥¶”–“ªø√ ˜”ΫΩCD£¨ADµƒæ‡¿Î∑÷± «15m∫Õ6m£¨“™Ω´’‚ø√ ˜Œß‘⁄ª®‘∞ƒ⁄£®∫¨±flΩÁ£¨≤ªøº¬« ˜µƒ¥÷œ∏£©£¨‘Úª®‘∞√ʪ˝Sµƒ◊Ó¥Û÷µŒ™£®°°°°£©
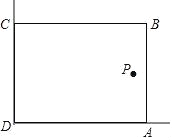
A. 193 B. 194 C. 195 D. 196
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ BD «°˜ABC µƒΩ«∆Ω∑÷œfl£¨ AE°Õ BD £¨¥π◊„Œ™ F £¨»Ù°œABC£Ω35°„£¨°œ C£Ω50°„£¨‘Ú°œCDE µƒ∂» ˝Œ™£® £©
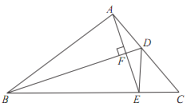
A.35°„B.40°„C.45°„D.50°„
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº( Ææ≈)£¨”√Àƒ∏ˆ¬›ÀøΩ´ÀƒÃı≤ªø…Õ‰«˙µƒƒæÃıŒß≥…“ª∏ˆƒæøÚ£¨≤ªº∆¬›Àø¥Û–°£¨∆‰÷–œ‡¡⁄¡Ω¬›Àøµƒæ‡¿Î“¿–ÚŒ™2°¢3°¢4°¢6£¨«“œ‡¡⁄¡ΩƒæÃıµƒº–Ω«æ˘ø…µ˜’˚°£»Ùµ˜’˚ƒæÃıµƒº–Ω« ±≤ª∆∆ªµ¥ÀƒæøÚ£¨‘Ú»Œ¡Ω¬›Àøµƒæ‡¿Î÷Æ◊Ó¥Û÷µŒ™∫Œ£ø

(A) 5 (B) 6 (C) 7 (D) 10
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨»ÁÕº£¨µ„A°¢D°¢B°¢E‘⁄Õ¨“ª÷±œfl…œ£¨AC=EF,AD=BE£¨°œA=°œE£¨
£®1£©«Û÷§£∫°˜ABC°’°˜EDF£ª
£®2£©µ±°œCHD=120°„£¨≤¬œÎ°˜HDBµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() °¢
°¢![]() ¡Ωµ„∑÷±‘⁄±fl
¡Ωµ„∑÷±‘⁄±fl![]() °¢
°¢![]() …œ£¨
…œ£¨![]() £¨
£¨![]() ”Î
”Î![]() œ‡Ωª”⁄µ„
œ‡Ωª”⁄µ„![]() £¨»Ù
£¨»Ù![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨‘Ú
£¨‘Ú![]() µƒ√ʪ˝Œ™________£Æ
µƒ√ʪ˝Œ™________£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() £¨“—÷™
£¨“—÷™![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() µƒ∂•µ„
µƒ∂•µ„![]() °¢
°¢![]() ∑÷±‘⁄±fl
∑÷±‘⁄±fl![]() °¢
°¢![]() …œ£¨µ±µ„
…œ£¨µ±µ„![]() ‘⁄±fl
‘⁄±fl![]() …œ‘À∂Ø ±£¨
…œ‘À∂Ø ±£¨![]() ÀÊ÷Æ‘⁄
ÀÊ÷Æ‘⁄![]() …œ‘À∂Ø£¨
…œ‘À∂Ø£¨![]() µƒ–Œ◊¥ º÷’±£≥÷≤ª±‰£¨‘⁄‘À∂صƒπ˝≥Ã÷–£¨µ„
µƒ–Œ◊¥ º÷’±£≥÷≤ª±‰£¨‘⁄‘À∂صƒπ˝≥Ã÷–£¨µ„![]() µΩµ„
µΩµ„![]() µƒ◊Ó–°æ‡¿ÎŒ™£® £©
µƒ◊Ó–°æ‡¿ÎŒ™£® £©

A. 5 B. 7 C. 12 D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com