如图.抛物线y=ax2+bx+3交x轴于A.B交y轴于C.抛物线的对称轴为x=1.OB=3AO(1)求抛物线的解析式,(2)若P为抛物线上一动点.M.N在直线l:y=-3x-6上.PM∥y轴.△PMN是以MN为底的等腰三角形.问是否存在这样的P.M.N三个点.使得△PMN的面积最小?若存在.求其最值,若不存在.请说明理由．中直线l沿抛物线的对称轴向上平移m个单位.设平移后的直线� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．如图，抛物线y=ax²+bx+3交x轴于A、B交y轴于C，抛物线的对称轴为x=1，OB=3AO
（1）求抛物线的解析式；
（2）若P为抛物线上一动点，M、N在直线l：y=-3x-6上，PM∥y轴，△PMN是以MN为底的等腰三角形，问是否存在这样的P、M、N三个点，使得△PMN的面积最小？若存在，求其最值；若不存在，请说明理由．
（3）将（2）中直线l沿抛物线的对称轴向上平移m个单位，设平移后的直线交抛物线于F、G两点（抛物线上的点F在点C的左边），连接OF、OC．问是否存在这样的直线，使得△FOG为钝角三角形？若存在，求m的值或取值范围；若不存在，请说明理由．

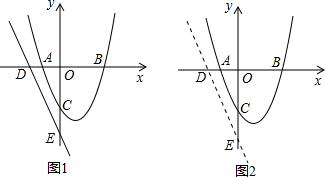
分析（1）根据对称轴方程x=$\frac{{x}_{1}{+x}_{2}}{2}$列方程即可求得结果．
（2）设P坐标为（x，x²-2x-3），则M点坐标为（x，-3x-6），过点P做MN的垂线，垂足为Q点，则由△PMN是以MN为底的等腰三角形，所以S_△PMN=2S_△PMQ，在Rt△APMQ中，MQ=3PQ，由勾股定理计算可得PQ=$\frac{\sqrt{10}}{10}$PM，QM=$\frac{3\sqrt{10}}{10}$PM，由S_△PMN=2S_△PMQ=$\frac{1}{2}$MN×PQ=$\frac{1}{2}$×2QM×PQ=QM×PQ=$\frac{3}{10}$PM²，因此只需求出PM的最小值即可，
（3）设平移后时直线解析式是y=-3x-6+m，向上平移当∠FOG是直角时，分别过F、G作FK⊥x轴于K，GL⊥x轴于L，得到△FXD∽△OLG，设出点F，G的坐标，代入比例式求得x₁x₂+y₁y₂=0，再把F，G点的坐标代入y=-3x-6+m，得到y₁=-3x₁-6+m，y₂=-3x₂-6+m．所以y₁y₂=9x₁x₂+（18-3m）（x₁+x₂）+（m-6）²，联立方程组消去y得x²+x+3-m=0，得到x₁十x₂=-1，x₁x₂=3-m，代入y₁y₂即可得到结果．

解答解：（1）设A（x₁，0），B（x₂，0），
∴OA=-x₁，OB=x₂，
∵OB=3AO，对称轴为x=1，
∴$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{{x}_{1}{-3x}_{1}}{2}$=1，
∴x₁=-1，x₂=3，
∴A（-1，0），B（3，0）
∴$\left\{\begin{array}{l}{0=a-b-3}\\{0=9a+3b-3}\end{array}\right.$得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$，
∴抛物线的解析式为：y=x²-2x-3；

（2）设P坐标为（x，x²-2x-3），则M点坐标为（x，-3x-6），
如图1，过点P做MN的垂线，垂足为Q点，则由△PMN是以MN为底的等腰三角形，
所以S_△PMN=2S_△PMQ，在Rt△APMQ中，MQ=3PQ，
由勾股定理计算可得PQ=$\frac{\sqrt{10}}{10}$PM，QM=$\frac{3\sqrt{10}}{10}$PM，
∴S_△PMN=2S_△PMQ=$\frac{1}{2}$MN×PQ=$\frac{1}{2}$×2QM×PQ=QM×PQ=$\frac{3}{10}$PM²，
因此只需求出PM的最小值即可，
PM=y_p-y_M=（ x²-2x-3）-（-3x-6）=x²+x+3=（x+$\frac{1}{2}$）2+$\frac{11}{4}$，
当x=-$\frac{1}{2}$时，PM有最小值$\frac{11}{4}$，
此时S_△PMN=$\frac{3}{10}$PM²=$\frac{363}{160}$；

（3）存在，
设平移后时直线解析式是y=-3x-6+m．
当直线过A、C两点时∠FOG是直角．此时m=3，
当直线过O点时，∠FOG=180°，此时m=6，
继续向上平移当∠FOG是直角时，
如图2，分别过F、G作FK⊥x轴于K，GL⊥x轴于L，
∴△FXD∽△OLG，
设F（x₁，y₁），G（x₂，y₂），
易得x₁x₂+y₁y₂=0，
∴y₁=-3x₁-6+m，y₂=-3x₂-6+m．y₁y₂=9x₁x₂+（18-3m）（x₁+x₂）+（m-6）²
∴$\left\{\begin{array}{l}{y=-3x-6+m}\\{y{=x}^{2}-2x-3}\end{array}\right.$消去y得x²+x+3-m=0，
∴x₁十x₂=-1，x₁x₂=3-m，
解得m=3（舍去）或16，
∴3＜m＜6或6＜m＜16．
∴当3＜m＜6或6＜m＜16时，△FOG为钝角三角形．

点评本题考查了求二次函数的解析式，二次函数的最值问题，三角形的面积，相似三角形的判定和性质，主要考查学生数形结合的数学思想方法，作出辅助线是做题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>