
����Ŀ����ͼ��ֱ��y=��x��4��������y=ax2+bx+c�ཻ��A��B���㣬����A��B����ĺ�����ֱ�Ϊ��1�ͩ�4���������߹�ԭ�㣮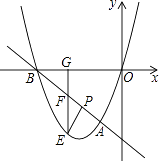
��1���������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�C��ʹ��ABCΪ���������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
��3������P���߶�AB�ϲ���A��B�غϵĶ��㣬����P��PE��OA���������ߵ������IJ��ֽ���һ��E������E��EG��x���ڵ�G����AB�ڵ�F����S��BGF=3S��EFP �� �� ![]() ��ֵ��
��ֵ��
���𰸡�
��1���⣺��A��B������ֱ��y=��x��4�ϣ��Һ�����ֱ�Ϊ��1����4��
��A����1����3����B����4��0����
�������߹�ԭ�㣬
��c=0��
��A��B����������������߽���ʽ�ɵ� ![]() �����
����� ![]() ��
��
�������߽���ʽΪy=x2+4x
��2���⣺�ߡ�ABCΪ���������Σ�
����AB=AC��AB=BC��CA=CB���������
�ٵ�AB=ACʱ������C��y���ϣ���C��0��y����
��AB= ![]() =3
=3 ![]() ��AC=
��AC= ![]() ��
��
��3 ![]() =
= ![]() �����y=��3��
�����y=��3�� ![]() ��y=��3+
��y=��3+ ![]() ��
��
��C��0����3�� ![]() ����0����3��
����0����3�� ![]() ����
����
����C��x����ʱ����C��x��0������AC= ![]() ��
��
�� ![]() =3
=3 ![]() �����x=��4��x=2����x=��4ʱ��B��C�غϣ���ȥ��
�����x=��4��x=2����x=��4ʱ��B��C�غϣ���ȥ��
��C��2��0����
�ڵ�AB=BCʱ������C��x���ϣ���C��x��0����
����AB=3 ![]() ��BC=|x+4|��
��BC=|x+4|��
��|x+4|=3 ![]() �����x=��4+3
�����x=��4+3 ![]() ��x=��4��3
��x=��4��3 ![]() ��
��
��C����4+3 ![]() ��0����4��3
��0����4��3 ![]() ��0����
��0����
����C��y���ϣ���C��0��y������BC= ![]() ��
��
�� ![]() =3
=3 ![]() �����y=
�����y= ![]() ��y=��
��y=�� ![]() ��
��
��C��0�� ![]() ����0����
����0���� ![]() ����
����
�۵�CB=CAʱ�����C���߶�AB�Ĵ�ֱƽ������y��Ľ��㴦��
��A����1����3����B����4��0����
���߶�AB���е�����Ϊ���� ![]() ����
���� ![]() ����
����
���߶�AB�Ĵ�ֱƽ���ߵĽ���ʽΪy=x+d��
�ੁ ![]() =��
=�� ![]() +d�����d=1��
+d�����d=1��
���߶�AB�Ĵ�ֱƽ���ߵĽ���ʽΪy=x+1��
��x=0�ɵ�y=1����y=0�����x=��1��
��C����1��0����0��1����
���Ͽ�֪�������������ĵ�C��������Ϊ��0����3�� ![]() ����0����3��
����0����3�� ![]() ����4+3
����4+3 ![]() ��0����4��3
��0����4��3 ![]() ��0����1��0����0��1����2��0����0��
��0����1��0����0��1����2��0����0�� ![]() ����0����
����0���� ![]() ��
��
��3���⣺����P��PQ��EF����EF�ڵ�Q������A��AD��x���ڵ�D��

��PE��OA��GE��AD��
���OAD=��PEG����PQE=��ODA=90�㣬
���PQE�ס�ODA��
�� ![]() =
= ![]() =3����EQ=3PQ��
=3����EQ=3PQ��
��ֱ��AB�Ľ���ʽΪy=��x��4��
���ABO=45��=��PFQ��
��PQ=FQ��BG=GF��
��EF=4PQ��
��GE=GF+4PQ��
��S��BGF=3S��EFP��
�� ![]() GF2=3��
GF2=3�� ![]() 4PQ2��
4PQ2��
��GF=2 ![]() PQ��
PQ��
�� ![]() =
= ![]() =
= ![]()
����������1����ֱ�߽���ʽ�ɷֱ����A��B��������꣬���ô���ϵ��������������߽���ʽ����2����AB=ACʱ����C��y���ϣ��ɱ�ʾ��AC�ij��ȣ�����������ꣻ��AB=BCʱ����֪��C��x���ϣ��ɱ�ʾ��BC�ij��ȣ�����������ꣻ��AC=BCʱ��C���߶�AB�Ĵ�ֱƽ������������Ľ��㴦��������߶�AB���е�����꣬����ô�ֱƽ���ߵĽ���ʽ��������C�����ꣻ��3������P��PQ��EF����EF�ڵ�Q������A��AD��x���ڵ�D����֤����PQE�ס�ODA�������EQ=3PQ���ٽ��F����ֱ��AB�ϣ������FQ=PQ��������EF=4PQ�����������ε�����Ĺ�ϵ�����GF��PQ�Ĺ�ϵ�������ñ�ֵ��
�����㾫����������Ĺؼ������������������ε����ʵ����֪ʶ�����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
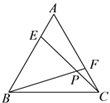
����Ŀ����ͼ����E����F�ֱ��ǵȱߡ�ABC�ı�AB��AC�ϵĵ㣬��BE=AF��CE��BF �ཻ�ڵ�P�����BPC�Ĵ�СΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ���� 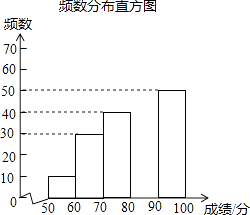
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 30 | 0.15 |
70��x��80 | 40 | n |
80��x��90 | m | 0.35 |
90��x��100 | 50 | 0.25 |
�����������Ϣ������������⣺
��1��m= �� n=��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ�������������Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ���š��ȣ����У�μ���α�����3000��ѧ���гɼ����š���Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڴ���ȫ���������й����У���������A��B���������ij·�ε�·�����̻����죬��֪����A������8�ã�B������3�ã���Ҫ950Ԫ��������A������5�ã�B������6�ã�����Ҫ800Ԫ��
��1������A��B��������ÿ�ø������Ԫ��
��2�����ǵ��̻�Ч�����ʽ���ת������A�����粻������50�ã������ڹ���������������ʽ��ܳ���7650Ԫ�����������������繲100�ã������ļ��ֹ�����
��3��ij�����ӳа���ֲ�������ֺ�һ��A������ɻ�Ǯ30Ԫ���ֺ�һ��B������ɻ�Ǯ20Ԫ���ڵڣ�2���ʵĸ��ֹ����У��ֺ���100�����磬��һ�ֹ�����������ֲ��Ǯ���٣����ٹ�Ǯ�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��b���dz�������k��0����ͼ���㣨1��0���ͣ�0��2����
��1������2��x��3ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m��n=4�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶��4��Բ�ܽǡ�C=60�㣬��Eʱֱ��AB�ӳ�����һ�㣬�ҡ�DEB=30�㣬��ͼ����Ӱ���ֵ����Ϊ �� 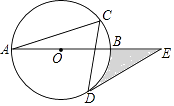
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ܳ�2.5m������б������ֱ��ǽ�ϣ���ʱ���㵽ǽ�ĵ˾���Ϊ0.7m�������Ӷ����»�0.4m�������㽫������
A��0.6mB��0.7m C��0.8mD��0.9m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��2��0��4����PΪ����������һ�㣬���Ӧ����Ϊx��
��1�������P����M��N�ľ�����ȣ���x���� ����
��2���������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����10�������ڣ����x��ֵ���������ڣ���˵�����ɣ�
��3�������P��ÿ����1����λ���ȵ��ٶȴӵ�O�����˶���ͬʱ��M�͵�N�ֱ���ÿ����2����λ���Ⱥ�ÿ����3����λ���ȵ��ٶ�Ҳ�����˶�����t����ʱ��P����M����N�ľ�����ȣ���t��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD��������С������һ��յأ���֪AB����2a+6b���ף�BC����8a+4b���ף�
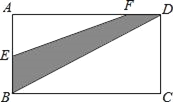
��1���ó�����ABCD������Ƕ���ƽ���ף�
��2����EΪAB�ߵ��е㣬DF��![]() BC���ִ�������Ӱ������ֲһƬ��ƺ����Ƭ��ƺ������Ƕ���ƽ���ף�
BC���ִ�������Ӱ������ֲһƬ��ƺ����Ƭ��ƺ������Ƕ���ƽ���ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com