
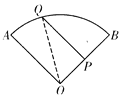
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
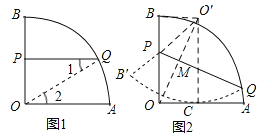
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

【答案】发现: 90°,10![]() ; 思考:(1)
; 思考:(1)![]() ;(2)25π100
;(2)25π100![]() +100;(3)点O到折痕PQ的距离为
+100;(3)点O到折痕PQ的距离为![]() .
.
【解析】发现:先判断出当PQ取最大时,点Q与点A重合,点P与点B重合,即可得出结论;
思考:(1)先判断出∠POQ=60°,最后用弧长用弧长公式即可得出结论;
(2)先在Rt△B'OP中,OP2+(10![]() 10)2=(10-OP)2,解得OP=10
10)2=(10-OP)2,解得OP=10![]() 10,最后用面积的和差即可得出结论.
10,最后用面积的和差即可得出结论.
探究:先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=![]() OO′=
OO′=![]() .
.
发现:∵P是半径OB上一动点,Q是![]() 上的一动点,
上的一动点,
∴当PQ取最大时,点Q与点A重合,点P与点B重合,
此时,∠POQ=90°,PQ=![]() =10
=10![]() ;
;
思考:(1)如图,连接OQ,
∵点P是OB的中点,
∴OP=![]() OB=
OB=![]() OQ.
OQ.
∵QP⊥OB,
∴∠OPQ=90°
在Rt△OPQ中,cos∠QOP=![]() ,
,
∴∠QOP=60°,
∴lBQ=![]()
(2)由折叠的性质可得,BP=B′P,AB′=AB=10![]() ,
,
在Rt△B'OP中,OP2+(10![]() 10)2=(10-OP)2
10)2=(10-OP)2
解得OP=10![]() 10,
10,
S阴影=S扇形AOB/span>-2S△AOP=![]()
=25π100![]() +100;
+100;
探究:如图2,找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,
则OM=O′M,OO′⊥PQ,O′P=OP=3,点O′是![]() 所在圆的圆心,
所在圆的圆心,
∴O′C=OB=10,
∵折叠后的弧QB′恰好与半径OA相切于C点,
∴O′C⊥AO,
∴O′C∥OB,
∴四边形OCO′B是矩形,
在Rt△O′BP中,O′B=![]() ,
,
在Rt△OBO′K,OO′=![]() ,
,
∴OM=![]() OO′=
OO′=![]() ×
×![]() =
=![]() ,
,
即O到折痕PQ的距离为![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
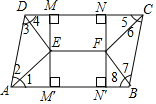
【题目】如图,在ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.
(1)求证:四边形EFNM是矩形;
(2)已知:AE=4,DE=3,DC=9,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
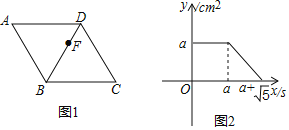
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
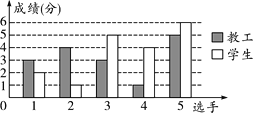
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华发现某月的日历中一个有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
(1)此日历中能画出 个十字框?
(2)若a+b+c+d=84,求k的值;
(3)是否存在k的值,使得a+b+c+d=108,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
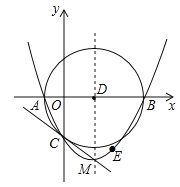
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
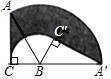
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为_____(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
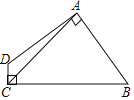
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com