[题目]如果一个等腰三角形一条腰上的高等于另一腰的一半.则该等腰三角形的底角的度数．题目和参考答案——青夏教育精英家教网—

【题目】如果一个等腰三角形一条腰上的高等于另一腰的一半，则该等腰三角形的底角的度数_____．

【答案】15°或75°

【解析】

因为三角形的高有三种情况，而直角三角形不合题意，故舍去，所以应该分两种情况进行分析，从而得到答案．

(1)当等腰三角形是锐角三角形时，腰上的高在三角形内部，如图，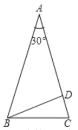

BD为等腰三角形ABC腰AC上的高,并且BD=AB，根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角为30°,此时底角为75°；
(2)当等腰三角形是钝角三角形时，腰上的高在三角形外部，如图，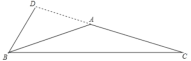

BD为等腰三角形ABC腰AC上的高,并且BD=AB，根据直角三角形中30°角的对边等于斜边的一半的逆用,可知顶角的邻补角为30°,此时顶角是150°，底角为15°.
故答案为：15°或75°.

练习册系列答案

金榜一号同步单元全程达标测试AB卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】为保护和改善环境，发展新经济，国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展，为响应号召，某市某汽车专卖店销售A，B两种型号的新能源汽车共25辆，这两种型号的新能源汽车的进价、售价如下表：

	进价万元辆	售价万元辆
A型	10
B型	15

如何进货，进货款恰好为325万元？

如何进货，该专卖店售完A，B两种型号的新能源汽车后获利最多且不超过进货价的，此时利润为多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图1，抛物线与x轴交于，两点，与y轴交于点C，点D为顶点．

求抛物线解析式及点D的坐标；

若直线l过点D，P为直线l上的动点，当以A、B、P为顶点所作的直角三角形有且只有三个时，求直线l的解析式；

如图2，E为OB的中点，将线段OE绕点O顺时针旋转得到，旋转角为，连接、，当取得最小值时，求直线与抛物线的交点坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，四边形ABCD中，对角线AC⊥BD于点O，且AO=BO=4，CO=8，∠ADB=2∠ACB，则四边形ABCD的面积为（）

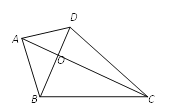
A.48B.42C.36D.32

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始以1cm/s的速度沿AB边向点B运动，点Q从点B以2cm/s的速度沿BC边向点C运动，如果P、Q同时出发，设运动时间为ts，
（1）当t=2时，求△PBQ的面积；
（2）当t=时，试说明△DPQ是直角三角形；
（3）当运动3s时，P点停止运动，Q点以原速立即向B点返回，在返回的过程中，DP是否能平分∠ADQ？若能，求出点Q运动的时间；若不能，请说明理由．