
【题目】在平面直角坐标系![]() 中,三角形
中,三角形![]() 的三个顶点分别是
的三个顶点分别是![]() ,
,![]() ,
,![]()
(1)在所给的网格图中,画出这个平面直角坐标系;
(2)点![]() 经过平移后对应点为
经过平移后对应点为![]() ,将三角形
,将三角形![]() 作同样的平移得到三角形
作同样的平移得到三角形![]() .
.
①画出平移后的三角形![]() ;
;
②若![]() 边上一点
边上一点![]() 经过上述平移后的对应点为
经过上述平移后的对应点为![]() ,用含
,用含![]() ,
,![]() 的式子表示点
的式子表示点![]() 的坐标;(直接写出结果即可)
的坐标;(直接写出结果即可)
③求三角形![]() 的面积.
的面积.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
一般的,如果一个正数x的平方等于a,即x2=a,那么正数x就叫做a的算术平分根,记作![]() (即
(即![]() ),如
),如![]() ,3就叫做9的算术平方根.
,3就叫做9的算术平方根.
(1)计算下列各式的值:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)观察(1)中的结果,![]() ,
,![]() ,
,![]() 这三个数之间存在什么关系?________________________
这三个数之间存在什么关系?________________________
(3)由(2)得出的结论猜想:![]() ________(
________(![]() ,
,![]() );
);
(4)根据(3)计算:![]() ________,
________,![]() ________,
________,![]() =________(写最终结果)
=________(写最终结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
摸到红球 次数m | 151 | 221 | 289 | 358 | 429 | 497 | 571 | 702 |
摸到红球 频率 | 0.75 | 0.74 | 0.72 | 0.72 | 0.72 | 0.71 | a | b |
(1)表格中a=_____;(精确到0.01)
(2)估计从袋子中摸出一个球恰好是红球的概率约为______;(精确到0.1)
(3)如果袋子中有7个红球,那么袋子中除了红球,估计还有几个其他颜色的球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.

(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么△DCB的面积是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在![]() 的正半轴上,点B的坐标为(3,4)一次函数
的正半轴上,点B的坐标为(3,4)一次函数![]() 的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是![]() 轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下: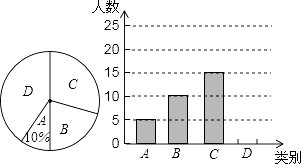
请结合图中信息解答下列问题:
(1)九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A的坐标为(-4,4),点B的坐标为(0,2).

(1)求直线AB的解析式;
(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC-OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M(-4,0)和N(2,0)是x轴上的两个点,点P是直线AB上一点.当△PMN是直角三角形时,请求出满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
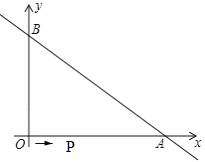
【题目】如图,直线![]() 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)则A点的坐标为_____,B两点的坐标为______;
(2)当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为______;
(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com