
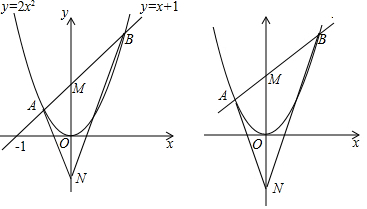
分析 (1)①联立直线和抛物线解析式可求得A、B两点的坐标;②过A作AC⊥y轴于C,过B作BD⊥y轴于D,可分别求得∠ANM和∠BNM的正切值,可证得结论;
(2)当k=0时,由对称性可得出结论;当k≠0时,过A作AE⊥y轴于E,过B作BF⊥y轴于F,设$A({x_1},a{x_1}^2)$、B$({x_2},a{x_2}^2)$,联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得$\frac{NF}{BF}=\frac{NE}{AE}$,则可证明Rt△AEN∽Rt△BFN,可得出结论.
解答 解:
(1)①由已知得2x2=x+1,解得$x=-\frac{1}{2}$或x=1,
当$x=-\frac{1}{2}$时,$y=\frac{1}{2}$,当x=1时,y=2,
∴A、B两点的坐标分别为($-\frac{1}{2}$,$\frac{1}{2}$),( 1,2);
②如图1,过A作AC⊥y轴于C,过B作BD⊥y轴于D,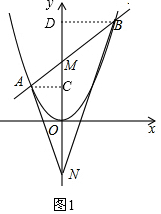
由①及已知有A($-\frac{1}{2}$,$\frac{1}{2}$),B( 1,2),且OM=ON=1,
∴$tan∠ANM=\frac{AC}{CN}=\frac{{\frac{1}{2}}}{{1+\frac{1}{2}}}=\frac{1}{3}$,$tan∠BNM=\frac{BD}{DN}=\frac{1}{1+2}=\frac{1}{3}$,
∴tan∠ANM=tan∠BNM,
∴∠ANM=∠BNM;
(2)∠ANM=∠BNM成立,
①当k=0,△ABN是关于y轴的轴对称图形,
∴∠ANM=∠BNM;
②当k≠0,根据题意得:OM=ON=b,设$A({x_1},a{x_1}^2)$、B$({x_2},a{x_2}^2)$.
如图2,过A作AE⊥y轴于E,过B作BF⊥y轴于F,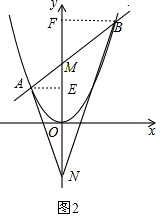
由题意可知:ax2=kx+b,即ax2-kx-b=0,
∴${x_1}+{x_2}=\frac{k}{a},{x_1}{x_2}=-\frac{b}{a}$,
∵$\frac{NF}{BF}-\frac{NE}{AE}=\frac{{b+a{x_2}^2}}{x_2}-\frac{{b+a{x_1}^2}}{{-{x_1}}}$=$\frac{{b{x_1}+a{x_1}{x_2}^2+b{x_2}+a{x_2}{x_1}^2}}{{{x_1}{x_2}}}$=$\frac{{({x_1}+{x_2})(a{x_1}{x_2}+b)}}{{{x_1}{x_2}}}$=$\frac{{\frac{k}{a}[a•(-\frac{b}{a})+b]}}{{(-\frac{b}{a})}}=0$,
∴$\frac{NF}{BF}=\frac{NE}{AE}$,
∴Rt△AEN∽Rt△BFN,
∴∠ANM=∠BNM.
点评 本题为二次函数的综合应用,涉及函数图象的交点、三角函数的定义、根与系数的关系、相似三角形的判定和性质等知识.在(1)②中求得两角的正切值是解题的关键,在(2)中利用根与系数的关系,整理求得$\frac{NF}{BF}=\frac{NE}{AE}$,是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
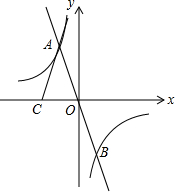 如图,正比例函数y1=-3x的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点.点C在x轴负半轴上,AC=AO,△ACO的面积为12.
如图,正比例函数y1=-3x的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点.点C在x轴负半轴上,AC=AO,△ACO的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测某批次灯泡的使用寿命,适宜用全面调查 | |
| B. | 可能性是1%的事件在一次试验中一定不会发生 | |
| C. | 数据3,5,4,1,-2的中位数是4 | |
| D. | “367人中有2人同月同日出生”为必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com