
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
【答案】A
【解析】解:连接OE,OF,ON,OG, 在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5﹣2﹣MN=3﹣MN,
在Rt△DMC中,DM2=CD2+CM2 ,
∴(3+NM)2=(3﹣NM)2+42 ,
∴NM= ![]() ,
,
∴DM=3+ ![]() =
= ![]() ,
,
故选A.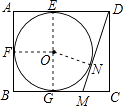
连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=4,由于AD,AB,BC分别与⊙O相切于E,F,G三点得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=2,由勾股定理列方程即可求出结果.


科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.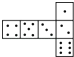 B.
B.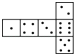 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
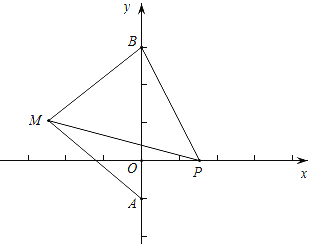
【题目】如图,在平面直角坐标系中,已知A(0,﹣1),B(0,3),点M为第二象限内一点,且点M的坐标为(t,1).
(1)请用含t的式子表示△ABM的面积;
(2)当t=﹣2时,在x轴的正半轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
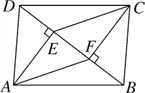
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则
(k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则![]() _________
_________![]() (填“>”“=”或“<”),若
(填“>”“=”或“<”),若![]() =2,则函数解析式为_________.
=2,则函数解析式为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,再解答问题:
-5![]() +7
+7![]() =-5+(-
=-5+(-![]() )+7+
)+7+![]() =[(-5)+7]+[(-
=[(-5)+7]+[(-![]() )+
)+![]() ]=2+
]=2+![]() =2
=2![]() .
.
上述方法叫做拆项法,依照上述方法计算:
(1)7![]() +(-7
+(-7![]() );
);
(2)(-2018![]() )+(-2017
)+(-2017![]() )+4036
)+4036![]() +(-1
+(-1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
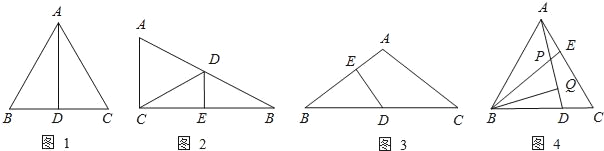
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com