
(8分)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=,求EF的长.
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
 ,连接BO、ED,有BO∥ED,作弦EF⊥AC于G,连接DF.
,连接BO、ED,有BO∥ED,作弦EF⊥AC于G,连接DF.| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
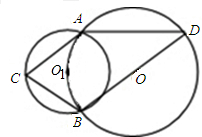 如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.
如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
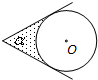 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )A、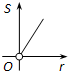 | B、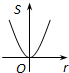 | C、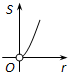 | D、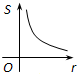 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )
(2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )查看答案和解析>>
科目:初中数学 来源: 题型:
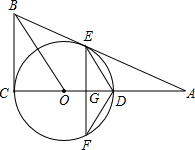 (2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
(2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.| 3 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com