练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知直线l1：y＝－4x＋8和直线l2：y＝2x－4．

    (1)在平面直角坐标系中画出这两条直线；

    (2)观察图象，求出直线l1和l2的交点坐标；

    (3)求不等式－4x＋8＞2x－4的解集．

    答案：
    解析：

    　　解：(1)图略．

    　　(2)由图象可以看出，直线l1和直线l2的交点坐标是(2，0)．

    　　(3)观察图象可知，不等式的解集为x＜2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2011年四川省攀枝花市中考数学试卷 题型：022

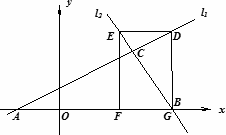
    如图，已知直线l1：y＝x＋与直线l2：y＝－2x＋16相交于点C，直线l1、l2分别交x轴于A、B两点，矩形DEFG的顶点D、E分别在l1、l2上，顶点F、G都在x轴上，且点G与B点重合，那么S矩形DEFG∶S△ABC＝________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读理解：对于任意正实数a、b，∵(－)2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.

    结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.  根据上述内容，回答下列问题：

    （1）若m＞0，只有当m＝       时，m＋有最小值         ；

    若m＞0，只有当m＝       时，2m＋有最小值        .

    （2）如图，已知直线L1：y＝x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝

    （x>0）相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试

    求当线段CD最短时，点A、B、C、D围成的四边形面积.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读理解：对于任意正实数a、b，∵(－)2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
    结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.  根据上述内容，回答下列问题：
    （1）若m＞0，只有当m＝      时，m＋有最小值        ；
    若m＞0，只有当m＝      时，2m＋有最小值       .
    （2）如图，已知直线L1：y＝x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
    （x>0）相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试
    求当线段CD最短时，点A、B、C、D围成的四边形面积.

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省江阴华士片八年级下学期期中考试数学卷（带解析） 题型：解答题

    阅读理解：对于任意正实数a、b，∵(－)2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
    结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.  根据上述内容，回答下列问题：
    （1）若m＞0，只有当m＝      时，m＋有最小值        ；
    若m＞0，只有当m＝      时，2m＋有最小值       .
    （2）如图，已知直线L1：y＝x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
    （x>0）相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试
    求当线段CD最短时，点A、B、C、D围成的四边形面积.

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省江阴华士片八年级下学期期中考试数学卷（解析版） 题型：解答题

    阅读理解：对于任意正实数a、b，∵(－)2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.

    结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.   根据上述内容，回答下列问题：

    （1）若m＞0，只有当m＝       时，m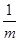＋有最小值         ；

    若m＞0，只有当m＝       时，2m＋有最小值        .

    （2）如图，已知直线L1：y＝x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝

    （x>0）相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试

    求当线段CD最短时，点A、B、C、D围成的四边形面积.

     

    查看答案和解析>>

    同步练习册答案