
科目:初中数学 来源: 题型:解答题
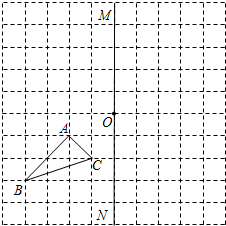 在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么CD的长度为( )cm.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么CD的长度为( )cm.| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
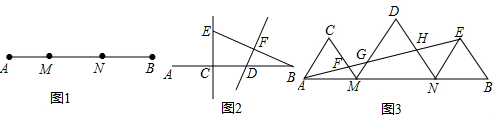
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
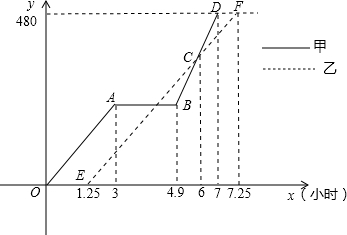 十一黄金周期间,甲、乙两个家庭相约到480km外的风景区“自驾游”,乙家庭由于要携带一些旅游用品,比甲家庭迟出发1.25h(从甲家庭出发时开始计时),甲、乙两个家庭所走的路程y甲(km)、y乙(km)与时间x(h)之间的函数关系图象如图所示,请根据图象所提供的信息解决下列问题:
十一黄金周期间,甲、乙两个家庭相约到480km外的风景区“自驾游”,乙家庭由于要携带一些旅游用品,比甲家庭迟出发1.25h(从甲家庭出发时开始计时),甲、乙两个家庭所走的路程y甲(km)、y乙(km)与时间x(h)之间的函数关系图象如图所示,请根据图象所提供的信息解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
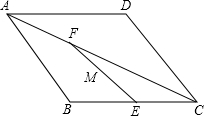 在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.
在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com