
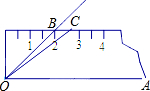
 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 分析 过点B作BD⊥OA于D,过点C作CE⊥OA于E.首先在等腰直角△BOD中,得到BD=OD=2cm,则CE=2cm,然后在直角△COE中,根据正切函数的定义即可求出OE的长度.
解答  解:过点B作BD⊥OA于D,过点C作CE⊥OA于E.
解:过点B作BD⊥OA于D,过点C作CE⊥OA于E.
在△BOD中,∠BDO=90°,∠DOB=45°,
∴BD=OD=2cm,
∴CE=BD=2cm.
在△COE中,∠CEO=90°,∠COE=37°,
∵tan37°=$\frac{CE}{OE}$≈0.75,∴OE≈2.7cm.
∴OC与尺上沿的交点C在尺上的读数约为2.7cm.
故答案为2.7.
点评 本题考查了解直角三角形的应用,属于基础题型,难度中等,通过作辅助线得到CE=BD=2cm是解题的关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com