
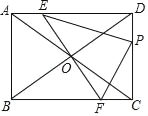
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.
【答案】(1)PC=3﹣x,FC=x;(2)当x=![]() 时,△PEF面积的最小值为
时,△PEF面积的最小值为![]() ;(3)PE⊥PF不成立理由见解析.
;(3)PE⊥PF不成立理由见解析.
【解析】
(1)由矩形的性质可得AD∥BC,DC=AB=3,AO=CO,可证△AEO≌△CFO,可得AE=CF=x,由DP=AE=x,可得PC=3﹣x;
(2)由S△EFP=S梯形EDCF﹣S△DEP﹣S△CFP,可得S△EFP=x2﹣![]() x+6=(x﹣
x+6=(x﹣![]() )2+
)2+![]() ,根据二次函数的性质可求△PEF面积的最小值;
,根据二次函数的性质可求△PEF面积的最小值;
(3)若PE⊥PF,则可证△DPE≌△CFP,可得DE=CP,即3﹣x=4﹣x,方程无解,则不存在x的值使PE⊥PF.
(1)∵四边形ABCD是矩形
∴AD∥BC,DC=AB=3,AO=CO
∴∠DAC=∠ACB,且AO=CO,∠AOE=∠COF
∴△AEO≌△CFO(ASA)
∴AE=CF
∵AE=x,且DP=AE
∴DP=x,CF=x,DE=4﹣x,
∴CP=3﹣x,PC=CD﹣DP=3﹣x
故答案为:3﹣x,x
(2)∵S△EFP=S梯形EDCF﹣S△DEP﹣S△CFP,
∴S△EFP=![]()
=x2﹣![]() x+6=(x﹣
x+6=(x﹣![]() )2+
)2+![]()
∴当x=![]() 时,△PEF面积的最小值为
时,△PEF面积的最小值为![]() .
.
(3)不成立
理由如下:若PE⊥PF,则∠EPD+∠FPC=90°
又∵∠EPD+∠DEP=90°
∴∠DEP=∠FPC,且CF=DP=AE,∠EDP=∠PCF=90°
∴△DPE≌△CFP(AAS)
∴DE=CP
∴3﹣x=4﹣x
则方程无解,
∴不存在x的值使PE⊥PF,
即PE⊥PF不成立.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
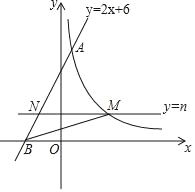
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣![]() <0的解集;
<0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
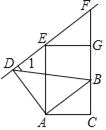
【题目】如图,在△ABC中,∠C=90°,AB=10,AC=8,将线段AB绕点A按逆时针方向旋转90°到线段AD.△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(I)求∠1的大小.
(Ⅱ)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
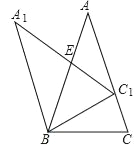
【题目】如图,在△ABC中,AB=AC,∠C=72°,△ABC绕点B逆时针旋转,当点C的对应点C1落在边AC上时,设AC的对应边A1C1与AB的交点为E,则∠BEC1=___°.
查看答案和解析>>
科目:初中数学 来源: 题型:
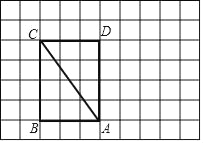
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D都在格点上.
(Ⅰ)AC的长为 ;
(Ⅱ)将矩形ABCD绕点A顺时针旋转得矩形AEFG,其中,点C的对应点F落在格线AD的延长线上,请用无刻度的直尺在网格中画出矩形AEFG,并简要说明点E,G的位置是如何找到的. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有5个只有颜色不同的球,其中3个黄球,2个黑球.
(1)求从袋中同时摸出的两个球都是黄球的概率;
(2)现将黑球和白球若干个(黑球个数是白球个数的2倍)放入袋中,搅匀后,若从袋中摸出一个球是黑球的概率是![]() ,求放入袋中的黑球的个数.
,求放入袋中的黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
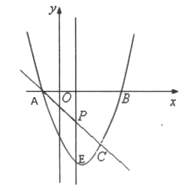
【题目】如图,抛物线![]() 与
与![]() 轴交
轴交![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),直线
点左侧),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,其中
两点,其中![]() 点的横坐标为2.
点的横坐标为2.
(1)求![]() 、
、![]() 两点的坐标及直线
两点的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 点作
点作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() 点,求线段
点,求线段![]() 长度的最大值;
长度的最大值;
(3)点![]() 是抛物线上的动点,在
是抛物线上的动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的
四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的![]() 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
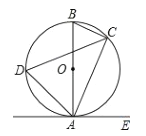
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com