
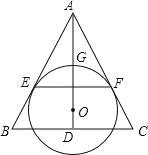
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC 分别相切于E,F两点.
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用等腰三角形的性质先判断AD是∠CAB的平分线,再根据切线长定理得到AE=AF,接着利用等腰三角形的性质判断AD⊥EF,然后根据平行线的判定可得到结论;
(2)先证明AD是EF的垂直平分线得到O在AD上;连结OE,OM,再根据切线的性质得到OE⊥AE,接着证明△ABC和△AEF都是等边三角形,则根据等边三角形的性质和含30度的直角三角形三边的关系计算出OE、AO,再利用勾股定理计算出OD,然后根据等边三角形的面积公式,利用四边形EBCF的面积=S△ABC-S△AEF进行计算即可.
试题解析:(1)∵△ABC是等腰三角形,AD⊥BC,
∴AD是∠CAB的平分线,
又∵☉O分别与AB,AC相切于点E,F,
∴AE=AF,
∴AD⊥EF,
∴EF∥BC;
(2)由(1)知,AE=AF,AD⊥EF,
∴AD是EF的垂直平分线,
∴O在AD上;
连结OE,OM,
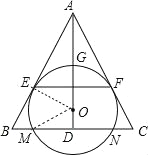
∵AB为切线,
∴OE⊥AE,
∴AG=OG=OE,
即AO=2OE,
∴∠OAE=30°,
∴∠EAF=60°,
∴△ABC和△AEF都是等边三角形,
∴AE=2![]() ,
,
∴OE=![]() AE=2,AO=2OE=4,
AE=2,AO=2OE=4,
∵OM=OE=2,DM=![]() MN=
MN=![]() ,
,
∴OD=![]() =1,
=1,
∴AD=AO+OD=5,
∴BD=![]() AD=
AD=![]() ,
,
∴AB=2BD=![]() ,
,
∴四边形EBCF的面积=S△ABC-S△AEF
=![]() (
(![]() )2-
)2-![]() ×(2
×(2![]() )2
)2
=![]() .
.


科目:初中数学 来源: 题型:
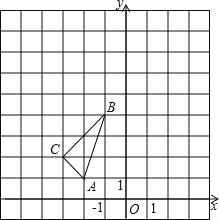
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C:y=ax2.
(1)若直线l1:y=x-1与抛物线C有且只有1个交点,求抛物线C的解析式.
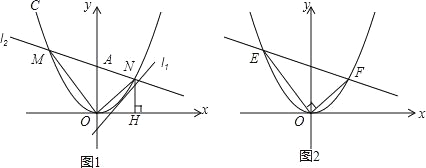
(2)如图1,在(1)的条件下,在y轴上有一点A(0,4),过点A作直线l2与抛物线C有两个交点M、N(N位于第一象限),过点N作x轴的垂线,垂足为H.试探究:是否存在l2,使△MON∽△NHO?若存在,求出l2的解析式;若不存在,说明理由.
(3)如图2,E、F为抛物线C(y=ax2)上两动点,始终满足OE⊥OF,连接EF,则直线EF是否恒过一定点G?若存在点G,直接写出G点坐标(用含a的坐标表示),若不存在,给予证明.
(参考结论:若直线l:y=kx+b上有两点(x1,y1)、(x2,y2),则斜率k=![]() ;当两直线l1、l2的斜率乘积k1k2=-1时,l1⊥l2)
;当两直线l1、l2的斜率乘积k1k2=-1时,l1⊥l2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON
(1)当直线l经过点D时,如图1,则OM、ON的数量关系为 ;
(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;
(3)当直线l与线段DC的延长线交于点P时,请在图3中作出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列式计算
(1)-个数与-5的差为-8,求这个数;
(2)-个数与9的差为-5,求这个数.
(3)温度由-9℃上升了3℃后的温度是多少?
(4)甲地的海拔是-63米,乙地比甲地高24米,则乙地的海拔为多少?
(5)土星表面夜间的平均气温为-150℃,白天的平均气温比夜间高27℃,那么白天的平均气温是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
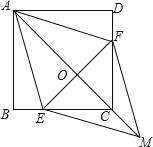
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com