
分析 (1)由三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,根据“最优组合”的定义即可求解;
(2)由三位“善雅数”的定义,可得a为偶数,且2+x+y是3的倍数,且2+x+y<30,又由m的各位数字之和为一个完全平方数,可得2+x+y=32=9,继而求得答案.
解答 (1)证明:∵三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,
∴重新排序后:其中两个数位上数字的和是一个数位上的数字的2倍,
∴a+c-2b=0,
∴F(t)=0;
∵(2)∵m=200+10x+y是“善雅数”,
∴x为偶数,且2+x+y是3的倍数,
∵x<10,y<10,
∴2+x+y<30,
∵m的各位数字之和为一个完全平方数,
∴2+x+y=32=9,
∴当x=0时,y=7,
当x=2时,y=5,
当x=4时,y=3,
当x=6时,y=1,
∴所有符合条件的“善雅数”有:207,225,243,261,
∴所有符合条件的“善雅数”中F(m)的最大值是|2+7-0×2|=9.
点评 此题考查了完全平方数的应用问题.注意掌握数的整除问题,注意掌握分类讨论思想的应用是解此题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
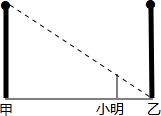 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
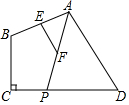 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )| A. | 线段EF的长先减小后增大 | B. | 线段EF的长不变 | ||
| C. | 线段EF的长逐渐增大 | D. | 线段EF的长逐渐减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com