
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 . 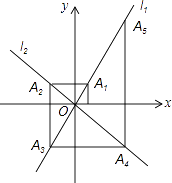
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】(12分)(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标_____(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如:如图①,若点A,B在数轴上分别对应的数为a,b(a<b),则AB的长度可以表示为AB=b-a.
请你用以上知识解决问题:
如图②,一个点从数轴上的原点开始,先向左移动2个单位长度到达A点,再向右移动3个单位长度到达B点,然后向右移动5个单位长度到达C点.
(1)请你在图②的数轴上表示出A,B,C三点的位置.
(2)若点A以每秒1个单位长度的速度向左移动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动,设移动时间为t秒.
①当t=2时,求AB和AC的长度;
②试探究:在移动过程中,3AC-4AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
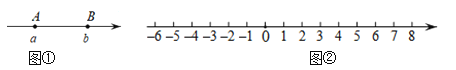
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在育民中学举办的“艺术节”活动中,八·二班学生成绩十分突出,小刚将全班获奖作品情况绘成如图的条形统计图(成绩为60分以上的都是获奖作品)
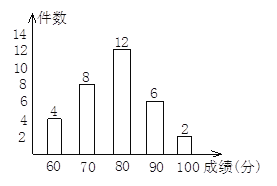
(1)请根据图表计算出八·二班学生有多少件作品获奖?
(2)用计算器求出八·二班获奖作品的平均成绩.
(3)求出这次活动中获奖作品成绩的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD平移后得到四边形A′B′C′D′
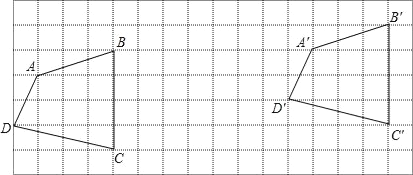
观察图形后完成下列问题:
(1)四边形ABCD先向 平移 个格,再向 平移 个格后得到四边形A′B′C′D′.
(2)图中有哪些相等的线段?有哪些平行的线段?
(3)S四边形ABCD和S四边形A′B′C′D′有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
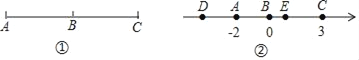
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=20cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点
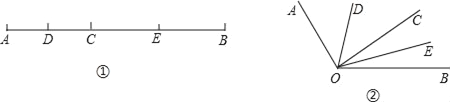
(1)若点C恰好是AB中点,则DE的长是多少?(直接写出结果)
(2)若BC=14cm,求DE的长
(3)试说明不论BC取何值(不超过20cm),DE的长不变
(4)知识迁移:如图②,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试求出∠DOE的大小,并说明∠DOE的大小与射线OC的位置是否有关?
查看答案和解析>>
科目:初中数学 来源: 题型:
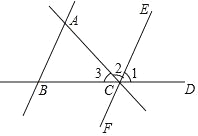
【题目】如图,直线BD上有一点C,则:
(1)∠1和∠ABC是直线AB,CE被直线_____所截得的____角;
(2)∠2和∠BAC是直线CE,AB被直线____所截得的_____角;
(3)∠3和∠ABC是直线_____、_____被直线_____所截得的____角;
(4)∠ABC和∠ACD是直线____、_____被直线_____所截得的角;
(5)∠ABC和∠BCE是直线_____、______被直线所截得的_____角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com