
 如图,已知∠ABE+∠DEB=180°,∠1=∠2,求证:∠F=∠G
如图,已知∠ABE+∠DEB=180°,∠1=∠2,求证:∠F=∠G分析 先根据∠ABE+∠DEB=180°得出AC∥ED,再由∠1=∠2得出∠FBE=∠BEG,故BF∥GE,由此可得出结论.
解答 证明:∵∠ABE+∠DEB=180°(已知),
∴AC∥ED(同旁内角互补,两线平行),
∴∠CBE=∠DEB(两线平行,内错角相等).
∵∠1=∠2(已知),
∴∠CBE-∠1=∠DEB-∠2(等式性质),即∠FBE=∠BEG,
∴BF∥EG(内错角相等,两线平行),
∴∠F=∠G(两线平行,内错角相等).
故答案为:同旁内角互补,两线平行;两线平行,内错角相等;∠FBE=∠BEG;BF∥EG,内错角相等,两线平行;两线平行,内错角相等.
点评 本题考查的是平行线的判定与性质,先根据题意得出AC∥ED,再由平行线的性质求解是解答此题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
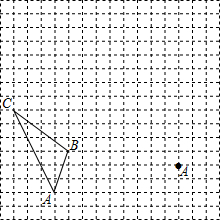 如图,在边长为1个单位长度的小正方形组成的网格中,
如图,在边长为1个单位长度的小正方形组成的网格中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 前香港中文大学校长高琨和George•Hockham首先提出光纤可以用于通讯传播的设想,高琨因此获得2009年诺贝尔物理学奖.如图是一光纤的简易结构图,它是通过光的全反射来实现光信号的传输,已知光纤经过光纤某一段的传输路线时,AB∥CD,有∠1=∠2,∠3=∠4,请解释进入的光线l为什么和第二次反射的光线m是平行的?请把下列解题过程补充完整.
前香港中文大学校长高琨和George•Hockham首先提出光纤可以用于通讯传播的设想,高琨因此获得2009年诺贝尔物理学奖.如图是一光纤的简易结构图,它是通过光的全反射来实现光信号的传输,已知光纤经过光纤某一段的传输路线时,AB∥CD,有∠1=∠2,∠3=∠4,请解释进入的光线l为什么和第二次反射的光线m是平行的?请把下列解题过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com