
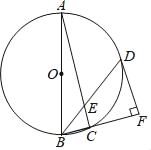
【题目】如图,△ABC是⊙O的内接圆,且AB是⊙O的直径,点D在⊙O上,BD平分∠ABC交AC于点E,DF⊥BC交BC延长线于点F.
(1)求证:DF是⊙O的切线.
(2)若![]() ,求DE的长.
,求DE的长.
【答案】(1)见解析(2)![]()
【解析】
(1)连接OD,根据角平分线的定义得到∠ABD=∠DBF,由等腰三角形的性质得到∠ABD=∠ODB,等量代换得到∠DBF=∠ODB,推出∠ODF=90°,根据切线的判定定理得到结论;
(2)连接AD,根据圆周角定理得到∠ADE=90°,根据角平分线的定义得到∠DBF=∠ABD,解直角三角形得到AD=3,求得DE=![]() .
.
解:(1)连接OD,
∵BD平分∠ABC交AC于点E,
∴∠ABD=∠DBF,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠DBF=∠ODB,
∵∠DBF+∠BDF=90°,
∴∠ODB+∠BDF=90°,
∴∠ODF=90°,
∴FD是⊙O的切线;
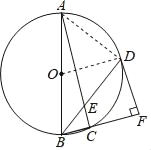
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADE=90°,
∵BD平分∠ABC交AC于点E,
∴∠DBF=∠ABD,
在Rt△ABD中,BD=4,
∵sin∠ABD=sin∠DBF=![]() ,
,
∴AD=3,
∵∠DAC=∠DBC,
∴sin∠DAE=sin∠DBC=![]() ,
,
在Rt△ADE中,sin∠DAC=![]() ,
,
∴DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,星期可卖出150件,现需降价处理,且经市场调查:每降价2元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价![]() 元、每星期售出商品的利润为
元、每星期售出商品的利润为![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有![]() 个红球,
个红球,![]() 个绿球和
个绿球和![]() 个白球,这些球除颜色外无其他差别,
个白球,这些球除颜色外无其他差别,
![]() 当
当![]() 时,从袋中随机摸出
时,从袋中随机摸出![]() 个球,摸到红球和摸到白球的可能性 (填“相同”或“不相同”);
个球,摸到红球和摸到白球的可能性 (填“相同”或“不相同”);
![]() 从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于
从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于![]() ,则
,则![]() 的值是 ;
的值是 ;
![]() 在
在![]() 的情况下,如果一次摸出两个球,请用树状图或列表法求摸出的两个球颜色不同的概率.
的情况下,如果一次摸出两个球,请用树状图或列表法求摸出的两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
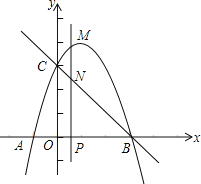
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,求线段MN的最大值;
(3)是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2020次旋转结束时,点D的坐标为( )
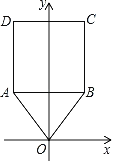
A.(﹣2,7)B.(7,2)C.(2,﹣7)D.(﹣7,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光![]() ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
(1)本次随机抽样的学生数是多少?A中![]() 值是多少?
值是多少?
(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com