
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
分析 (1)设出函数解析式,进一步代入求得函数解析式;
(2)利用销售利润=每千克的利润×销售量求得函数解析式,根据函数性质求最值.
解答 解:设y=kx+b,
∵点(25,2000),(24,2500)在图象上,
∴$\left\{\begin{array}{l}{2000=25k+b}\\{2500=24k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-500}\\{b=14500}\end{array}\right.$.
∴y=-500x+14500.
(2)W=(x-13)•y
=(x-13)•(-500x+14500)
=-500x2+21000x-188500
=-500(x-21)2+32000.
P与x的函数关系式为:P=-500x2+21000x-188500,
当销售价为21元/千克时,W的值最大为32000.
点评 此题考查二次函数的实际运用,掌握待定系数法求函数解析式,二次函数的性质以及基本的数量关系是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.
如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
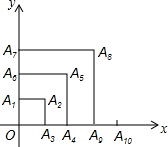 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )| A. | (0,672) | B. | (671,671) | C. | (672,672) | D. | (672,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com