
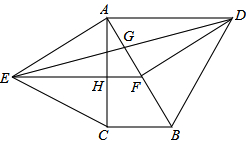
 如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.分析 (1)由SAS证明△ABC≌△EFA,即可得出EF=AB;
(2)证出EF=AB,AE=DF,即可得出结论;
(3)由平行四边形的性质得出AG=FG=$\frac{1}{2}$AF=$\frac{\sqrt{3}}{2}$,由勾股定理得出AE=AC=$\sqrt{3}$BC=3,EG=$\sqrt{A{E}^{2}+A{G}^{2}}$=$\sqrt{9+\frac{9}{4}}$=$\frac{3\sqrt{5}}{2}$,即可得出△AEG的周长.
解答 (1)证明:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴BF=AF,AB=2AF,
∴BC=AF,在△△EFA和△ABC中,$\left\{\begin{array}{l}{AE=AC}&{\;}\\{∠FEA=∠ACB}&{\;}\\{AF=BC}&{\;}\end{array}\right.$,
∴△EFA≌△ABC(SAS),
∴EF=AB;
(2)证明:∵△ABD是等边三角形,
∴AD=BD,
∵BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形;
(3)解:∵F为AB边的中点,
∴AF=$\frac{1}{2}$AB=$\sqrt{3}$,
∵四边形ADFE是平行四边形;
∴AG=FG=$\frac{1}{2}$AF=$\frac{\sqrt{3}}{2}$,
∵∠ACB=90°,∠BAC=30°,
∴BC=$\frac{1}{2}$AB=$\sqrt{3}$,
∴AE=AC=$\sqrt{3}$BC=3,
∵∠FAE=90°,
∴EG=$\sqrt{A{E}^{2}+A{G}^{2}}$=$\sqrt{9+\frac{9}{4}}$=$\frac{3\sqrt{5}}{2}$,
∴△AEG的周长=AE+EG+AG=3+$\frac{3\sqrt{5}}{2}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查了平行四边形的判定和性质,等边三角形的性质,直角三角形的性质,勾股定理以及全等三角形的判定和性质;本题综合性强,有一定难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
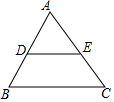 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )| A. | 54° | B. | 62° | C. | 64° | D. | 74° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com