
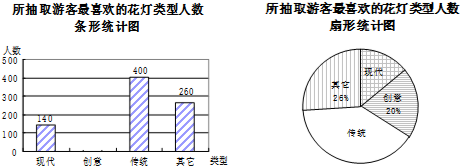
分析 (1)根据其他有260人占26%可以求得被调查的游客人数,根据传统所占的百分比再乘以360°,可以求得传统所对应的圆心角的度数;
(2)根据(1)中求得的数据可以得到选创意的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以得到“最喜欢现代型”花灯的人数.
解答 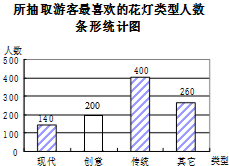 解:(1)本次抽取的游客人数为:260÷26%=1000,
解:(1)本次抽取的游客人数为:260÷26%=1000,
“传统”型所对应的圆心角为:$\frac{400}{1000}$×360°=144°,
故答案为:1000,144;
(2)选择“创意”的游客有:1000×20%=200(人),
补全的条形统计图如右图所示,
(3)100×$\frac{140}{1000}$=14(万人),
即“最喜欢现代型”花灯的游客有14万人.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≤1 | C. | 0<a≤1 | D. | -1≤a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
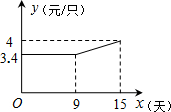 屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.
屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
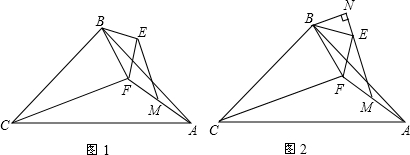
 如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com