
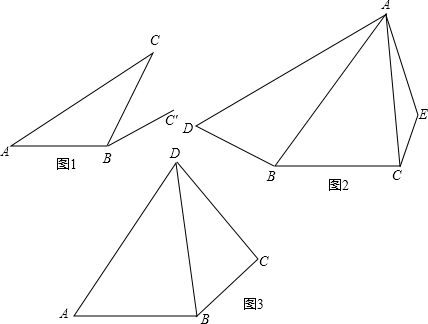
 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.分析 (1)根据直角三角形斜边的中线等于斜边的一半证得FC=FE即可,再证明∠CFE=60°,从而进行判断;
(2)根据∠B=60°,∠DEB=90°,可知BD=$\sqrt{2}$DE,又BD=$\sqrt{2}$CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠CDE等于旋转角,∠CDE=180°-∠BDE=180°-30°=150°.
解答 解:(1)∵∠ACB=90°,F是AD中点,
∴FC=$\frac{1}{2}$AD,
∵DE⊥AB,F是AD中点,
∴EF=$\frac{1}{2}$AD,
∴FC=FE,
∴△CEF是等腰三角形;
又EF=AF,CF=AF,故∠CFE=2∠CAB=60°
从而可知:△CEF是等边三角形.
(2)n=60°或135°
理由:①将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边AC上时,此时记为B'点(图请自画)
△B'CD为直角三角形,
又∵BD=$\sqrt{2}$CD,
故∠B'DC=45°;从而旋转角∠BDB'=180°-∠B'DC=180°-45°=135°
②当B'在边AB上上时,有DB=DB',又∠B=60°,故可知△DBB'为等边三角形,所以∠BDB'=60°;即n=60°
点评 本题主要考查了旋转的性质、直角三角形的性质、等腰三角形的判定等知识的综合运用,熟练的运用旋转的性质和直角三角形斜边的中线等于斜边的一半这一性质是解决问题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 6或10 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 公园里有一座小山供游人健身锻炼,上山台阶的截面如图所示,从山脚至山顶的台阶高度起起伏伏,而宽度除前两个台阶为4.3m外,其余每个台阶宽都为0.3米.
公园里有一座小山供游人健身锻炼,上山台阶的截面如图所示,从山脚至山顶的台阶高度起起伏伏,而宽度除前两个台阶为4.3m外,其余每个台阶宽都为0.3米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com