
����Ŀ����ͼ������ABC�������У�������ÿ��С�����εı߳���Ϊ1�����ν���λ�Ʊ任����ԳƱ任��ƽ�Ʊ任��õ���A3B3C3��
��1����ABC����A1B1C1��λ�Ʊȵ��� ��
��2���������л�����A1B1C1����y�����Գ�ͼ����A2B2C2��
��3����д����A3B3C3������A2B2C2����ƽ�Ƶõ��ģ�
��4�����P��x��y��Ϊ��ABC��һ�㣬���ξ����������α任��P�Ķ�Ӧ�������Ϊ ��

���𰸡�(1)![]() ����2��ͼ����������3����A3B3C3������A2B2C2��x������ƽ��2����λ������y������ƽ��2����λ�õ�����4������2x��2��2y+2����
����2��ͼ����������3����A3B3C3������A2B2C2��x������ƽ��2����λ������y������ƽ��2����λ�õ�����4������2x��2��2y+2����
�������������������1������λ��ͼ�οɵ�λ�Ʊȼ��ɣ���2��������Գ�ͼ�εĻ�������ͼ�μ��ɣ���3��������A3B3C3����A2B2C2�Ĺ�ϵ������仯���̼��ɣ���4���������α任���ɵó����꼴�ɣ�
�����������1������ABC����A1B1C1��λ�Ʊȵ���=![]() ��
��
��2����ͼ��ʾ
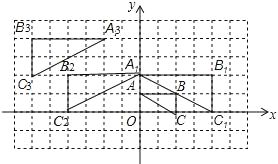
��3����A3B3C3������A2B2C2��x������ƽ��2����λ������y������ƽ��2����λ�õ���
��4����P��x��y��Ϊ��ABC��һ�㣬���ξ����������α任��P�Ķ�Ӧ�������Ϊ����2x��2��2y+2����


 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУҪ����һ֧��6��Ů����ɵ����Ƕӣ����꼶�������ѡ6��Ů�����ֱ���ɼӺ��ҶӲμ�ѡ�Σ�ÿλŮ��������ͳ����ͼ������ͳ�������±���
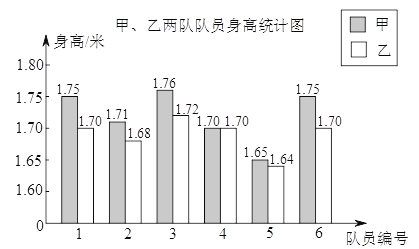
ƽ���� | ���� | ��λ�� | |
�� | 1.72 | 0.038 | |
�Ҷ� | 0.025 | 1.70 |
��1��������ߵ���λ����
��2�����Ҷ����ߵ�ƽ���������߲�С��1.70��Ƶ�ʣ�
��3�����ѡ�εı�������Խ����Խ�ã���ô�ס�������
����һ�ӽ���¼ȡ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
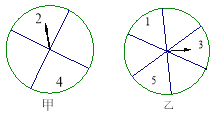
����Ŀ����ϲ������Ϸ��?��������һ��ת����Ϸ����ͼ��ʾ������ת����ָ������ÿһ�������ϵĻ�����ȣ���ͬʱ����ת���ס�������ת�̣�ת��ֹͣ��ָ���ָ��һ�����֣�����ָ�������������˻������п��ܵõ��IJ�ͬ�Ļ��ֱ�Ϊ_______________________������֮��Ϊ�����ĸ���Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У� ![]() ���ӳ�BC����E������AE��CD�ڵ�F��ʹ
���ӳ�BC����E������AE��CD�ڵ�F��ʹ![]()
![]() ��֤��
��֤�� ![]() ��
��
![]() ��֤��
��֤�� ![]() ��
��
![]() ��BFƽ��
��BFƽ��![]() ����д��
�����![]() ��
��![]() ��������ϵ______
��������ϵ______![]() ����֤��
����֤��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ���߶�������ϵ�����У�����������н�ƽ���ߣ������������湹��ȫ�������εĽ��˼·.�磺��ͼ1�У���![]() ��
��![]() ��ƽ����
��ƽ����![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() �ϣ���ʱ����
�ϣ���ʱ����![]() ��ȡ
��ȡ![]() ,����
,����![]() ������������ȫ�ȵ��ж�
������������ȫ�ȵ��ж�![]() ���������ȫ�������ΨS
���������ȫ�������ΨS![]() �ͨS
�ͨS![]() ,�ο�����ķ���������������⣺
,�ο�����ķ���������������⣺

��ͼ2���ڷǵȱߨS![]() �У�
�У� ![]() ,
, ![]() �ֱ���
�ֱ���![]() ��ƽ���ߣ���
��ƽ���ߣ���![]() ���ڵ�
���ڵ�![]() .��֤��
.��֤�� ![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��(1)P�ǵ���������A BC�ױ�BC�ϵ�һ�˶��㣬����P��BC�Ĵ��ߣ���AB�ڵ�Q����CA���ӳ����ڵ�R����۲�AR��AQ�������кι�ϵ����֤����IJ��롣
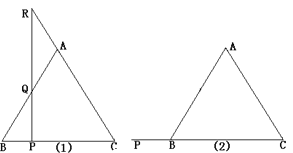
(2)�����P���ŵױ�BC���ڵ�ֱ�ߣ�����C��B�ķ����˶���CB���ӳ�����ʱ��(1)�����õĽ��ۻ�������������ͼ15(2)�����ͼ �Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DE��BC�� AB��CD��EΪAB���е㣬��A=��B�����н��ۣ���CD=AE����AC=DE����ACƽ�֡�BCD����O����DE���е㣻��AC=AB��������ȷ���ǣ�������
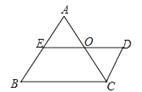
A. �٢ڢ� B. �٢ۢ� C. �ڢۢ� D. �ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС���о��ҹ��Ŵ����㷨ͳ�ڡ�������һ��ʫ�����ʿ������������ڿͶ��������У�һ���߿Ͷ��߿ͣ�һ���ſ�һ���գ�ʫ�к��������˼�ǣ����ÿһ��ͷ�ס7�ˣ���ô��7������ס�����ÿһ��ͷ�ס9�ˣ���ô�Ϳճ�һ�䷿��
��1����õ��пͷ����ټ䣿���Ͷ����ˣ�
��2������������������ͷ����и��������������ӣ�ÿ��ͷ��շ�20Ǯ����ÿ��ͷ������ס4�ˣ�һ���Զ��ͷ�18�����ϣ���18�䣩�����Ѱ�8���Żݣ���ʫ�С��ڿ͡��ٴ�һ����ס��������ζ��������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֽƬ��ABC��DE�۵�ʹ��A����A�䴦��λ�ã�
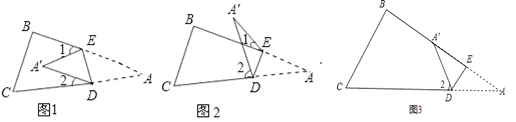
��1�����A�������ı���BCDE���ڲ�����ͼ1������A�����1+��2֮�����������������ϵ����˵�����ɣ�
��2�����A�������ı���BCDE��BE���ϣ���ʱͼ1�еġ�1��Ϊ0��ǣ�����ͼ3�����A�����2֮��Ĺ�ϵ�� ��
��3�����A�������ı���BCDE���ⲿ����ͼ2������ʱ��A�����1����2֮���ִ���������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com