
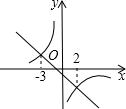
 ��������max{a��b}����a��bʱ��max{a��b}=a����a��bʱ��max{a��b}=b����max{-3��2}=2��
��������max{a��b}����a��bʱ��max{a��b}=a����a��bʱ��max{a��b}=b����max{-3��2}=2������ ��1������3��$\sqrt{7}$����֪������ɣ�
��2����������ó�$\frac{{k}_{1}}{x}$��k2x+b�����ͼ��������ɣ�
��3����Ϊ�����������2x+1��x-2ʱ����2x+1��x-2ʱ�������֪������ɣ�
��� �⣺��1��max{$\sqrt{7}$��3}=3��
�ʴ�Ϊ��3��
��2����max{$\frac{{k}_{1}}{x}$��k2x+b}=$\frac{{k}_{1}}{x}$��
��$\frac{{k}_{1}}{x}$��k2x+b��
���ͼ���֪��x��ȡֵ��ΧΪ-3��x��0��x��2��
��3����2x+1��x-2ʱ��max{2x+1��x-2}=2x+1��
��2x+1��x-2ʱ��max{2x+1��x-2}=x-2��
���� ���⿼����һ�κ����ͷ����������Ľ��������Ӧ�ã��ܶ��������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 24�� | C�� | 15�� | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
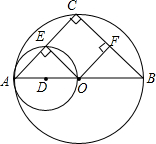 ��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O���ң���OAΪֱ���ġ�D��AC�ཻ�ڵ�E��
��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O���ң���OAΪֱ���ġ�D��AC�ཻ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
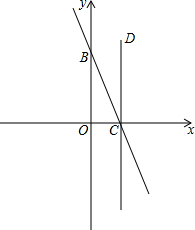 ��ͼ��ֱ��y=-2x+4��������ֱ���C��B���㣬����C��CD��x�ᣬ��P��x���·�ֱ��CD�ϵ�һ�㣬�ҡ�OCP���OBC���ƣ������P��˫���߽���ʽ��
��ͼ��ֱ��y=-2x+4��������ֱ���C��B���㣬����C��CD��x�ᣬ��P��x���·�ֱ��CD�ϵ�һ�㣬�ҡ�OCP���OBC���ƣ������P��˫���߽���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
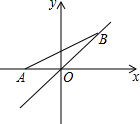 ��ͼ������A��-2��0��������B��ֱ��y=x���˶������߶�AB���ʱ����B������Ϊ��-1��-1����
��ͼ������A��-2��0��������B��ֱ��y=x���˶������߶�AB���ʱ����B������Ϊ��-1��-1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD�ı߳�Ϊ4����P��Q�ֱ���CD��AD���е㣬����E�ӵ�A���B�˶�������Bʱֹͣ�˶���ͬʱ������F�ӵ�P��������P��D��Q�˶�����E��F���˶��ٶ���ͬ�����E���˶�·��Ϊx����AEF�����Ϊy���ܴ��¿̻�y��x�ĺ�����ϵ��ͼ���ǣ�������
��ͼ��������ABCD�ı߳�Ϊ4����P��Q�ֱ���CD��AD���е㣬����E�ӵ�A���B�˶�������Bʱֹͣ�˶���ͬʱ������F�ӵ�P��������P��D��Q�˶�����E��F���˶��ٶ���ͬ�����E���˶�·��Ϊx����AEF�����Ϊy���ܴ��¿̻�y��x�ĺ�����ϵ��ͼ���ǣ�������| A�� | 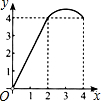 | B�� | 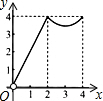 | C�� | 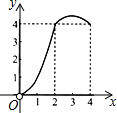 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
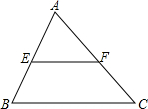 ��ͼ���ڡ�ABC�У�E��F�ֱ�ΪAB��AC���е㣬���AEF���ABC�����֮��Ϊ1��4��
��ͼ���ڡ�ABC�У�E��F�ֱ�ΪAB��AC���е㣬���AEF���ABC�����֮��Ϊ1��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com